Introducere

            În vara anului 1974, pe când eram student, am încercat să rezolv următoarea problemă: care este probabilitatea ca, aruncând o cutie de chibrituri pe o masă, ea să cadă pe faţa mare, cea mijlocie şi respectiv pe cea mică ? Dacă se putea, aş fi vrut să calculez aceste probabilităţi în funcţie de laturile a, b, c ale cutiei de chibrituri, rezultând astfel trei funcţii 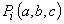 cu .

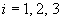            Mi-am confecţionat paralelipipede de lemn uşor, lemn greu, aluminiu şi fier de câteva (patru) dimensiuni dfierite şi am pornit experienţele. După câteva zeci de mii de aruncări am sistematizat rezultatele. Întâi am comparat frecvenţele apărute la cele patru tipuri de materiale cu ajutorul unor teste (Chi pătrat şi T); diferenţele între ele nu au fost suficient de mari ca să resping ipoteza că 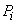 nu depinde de materialul din care sunt confecţionate paralelipipedele (dar nici destul de mici ca să o accept ! Teoria testelor statistice oripilează prin intuiţionismul său: de obicei, în majoritatea cazurilor practice, nu poţi admite la un nivel de semnificaţie cât de cât decent - 1% - o ipoteză dar, de multe ori nu o poţi respinge - cu acelaşi nivel de semnificaţie.) Am ales calea cea mai comodă, acceptând ipoteza; apoi am făcut o ipoteză asupra suprafeţei medii a cutiei de chibrituri care a părut bună - la o comparare vizuală -. În continuare am aplicat principiul informaţiei maxime (la sugestia prof. Guiaşu S.) care este o regulă metodologică în estimarea unei distribuţii de probabilităţi de genul următor: dintre toate repartiţiile posibile de probabilităţi care satisfac o condiţie dată (în cazul meu era suprafaţa medie, în care consideram ipoteza făcută corectă) trebuie aleasă aceea care asigură cea mai mare entropie. Nu îmi propun să-i discut valoarea epistemologică (de exemplu, dacă aplicam conceptul de energie informaţională am fi putut cere ca acest indicator să fie minim şi ar fi rezultat altă repartiţie de probabilităţi); principalul este că, folosindu-l am putut estima probabilităţile căutate. Estimarea făcută am comparat-o cu frecvenţele reale, folosind acelaşi test 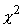 şi iarăşi am fost în aceeaşi situaţie ca înainte: nu îmi puteam permite să resping estimarea făcută la nivel de semnificaţie de 5%. Bineînţeles că am acceptat-o - altfel aş fi muncit în zadar - şi am prezentat lucrarea la o sesiune de comunicări studenţească în 1975.

            De atunci aproape în fiecare an mă întreb: a avut vreun sens tot ce am făcut ?

            Mai precis: are vreun sens obiectiv întrebarea „Care este probabilitatea ca ...”? în afară de acela de grad de încredere.

            Sau, într-o altă formulare: Enunţul 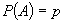 (probabilitatea evenimentului A este p) este verificabil sau falsificabil ? Este adevărat că, dacă A reprezintă apariţia stemei la o aruncare cu banul, 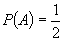 ? Este aceasta o lege a naturii sau o convenţie izvorâtă din motive de simetrie: „toată lumea va fi de acord că nu avem motive să considerăm că una din feţe este favorizată” sau „dacă feţele unui zar nu ar fi numerotate, ele nu ar putea fi deosebite una de alta; de aceea este „evident” că ele sunt la fel de probabile”. Mie nu mi se pare evident de loc.

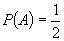
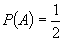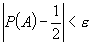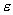            Ar fi bine dacă enunţul „ ” s-ar putea demonstra prin metode matematice. Adică, presupunând o repartiţie statistică a vitezelor iniţiale şi a coordonatelor centrului de greutate ale monezii, să se demonstreze că, în ipoteze foarte generale asupra densităţilor de repartiţie ale acestor mărimi, , sau măcar  pentru un  „foarte mic”. Din păcate, puterea de calcul a matematicii actuale nu permite stabilirea feţei pe care va cădea o monedă, chiar dacă se cunosc condiţiile iniţiale şi se neglijează frecarea cu aerul: nu este clar, fizic, ce se întâmplă când moneda interacţionează cu planul pe care este aruncată. Este o problemă de teoria elasticităţii foarte complicată în sine. Primul care s-a gândit la explicarea probabilităţilor aparente prin repartiţii „ascunse” a fost H. Poincaré (1912). El a numit-o „metoda funcţiilor arbitrare”. A fost continuat de Reichenbach, H. (1935), M. Frechet (1952) şi Hincin (1952)ş ultimul vedea în ea o armă de „luptă împotriva idealismului în teoria probabilităţilor”. Voi studia un exemplu în acest sens în Anexa 3. Deocamdată mă mulţumesc să remarc că acest mod de a pune problema pare să confirme părerea lui von Mises că „nu se pot trage concluzii probabiliste decât din premise probabiliste” şi că valoarea lui explicativă nu este foarte clară.

        La urma urmelor întrebarea care mă interesează este de natură ontologică: probabilitatea unui eveniment „există” ? Care este statutul ontic al conceptului de probabilitate ?

        Subiectul este spinos şi mult mai greu decât mi s-a părut la prima vedere. Mulţi gânditori de elită şi-au pus aceeaşi întrebare (ca să nu amintim decât pe Pascal, Bernoulli, Laplace, Cournot, von Mises, Poincaré, Reichenbach, Popper, De Finetti, Carnap, Onicescu) iar o incursiune în polemicile actuale privind interpretarea conceptului de probabilitate mi se pare temerară. Printre atâtea puncte de vedere contradictorii este greu să îţi faci o părere personală pe care să o argumentezi coerent.

Mi-am asumat sarcina modestă de a prezenta aceste puncte de vedere în măsura în care      le-am înţeles.