 ,
,
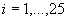 , au fost
următoarele: 14, 18, 24, 21, 20, 21, 23, 17, 21, 20, 14, 28, 18, 21, 25, 20,
19, 18, 23, 21, 18, 22, 15, 23, 23.
, au fost
următoarele: 14, 18, 24, 21, 20, 21, 23, 17, 21, 20, 14, 28, 18, 21, 25, 20,
19, 18, 23, 21, 18, 22, 15, 23, 23.ANEXA 1. DOUĂ EXEMPLE
EXEMPLUL 1.
Se aruncă
o monedă de 5 lei din aceeași poziție de pe masă. Apariția stemei a fost notată
cu 1, iar cea a banului cu 0. Experimentul s-a repetat de 1000 de ori. Frecvențele
absolute ale apariției stemei în serii de câte 40 de probe, notate 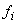 ,
,
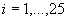 , au fost
următoarele: 14, 18, 24, 21, 20, 21, 23, 17, 21, 20, 14, 28, 18, 21, 25, 20,
19, 18, 23, 21, 18, 22, 15, 23, 23.
, au fost
următoarele: 14, 18, 24, 21, 20, 21, 23, 17, 21, 20, 14, 28, 18, 21, 25, 20,
19, 18, 23, 21, 18, 22, 15, 23, 23.
Frecvențele
mobile, cumulate în serii de 200 de probe (notate 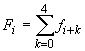 ) au fost:
) au fost:
97, 104, 109, 102, 102, 102, 95, 100, 101, 106, 112, 103, 102, 105, 101, 99, 102, 99, 99, 101, 101.
Frecvența
totală: 507. Se coroborează ipoteza că 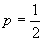 (nu se
poate respinge cu datele de care dispunem !). Frecvențele relative în serii
de 200 sunt extrem de stabile: au oscilat numai între 0.475 și 0.560 (sub 10%).
(nu se
poate respinge cu datele de care dispunem !). Frecvențele relative în serii
de 200 sunt extrem de stabile: au oscilat numai între 0.475 și 0.560 (sub 10%).
Să încercăm
să testăm ipoteza independenței aruncărilor. Dacă ar fi independente, frecvențele
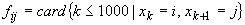 ar trebui
să fie cam egale
ar trebui
să fie cam egale 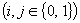 . La fel
și frecvențele
. La fel
și frecvențele 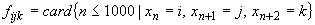 , i,
j, k
, i,
j, k 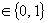 , ar trebui
să fie aproximativ egale. Între ele este relația evidentă
, ar trebui
să fie aproximativ egale. Între ele este relația evidentă 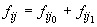 . Rezultatele
au fost cele din tabelul de mai jos (
. Rezultatele
au fost cele din tabelul de mai jos ( 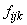 este la
intersecția liniei ij cu coloana k):
este la
intersecția liniei ij cu coloana k):
|
0 |
1 |
|
|
|
00 |
136 |
108 |
244 |
|
01 |
122 |
124 |
249 |
|
10 |
113 |
132 |
245 |
|
11 |
122 |
140 |
262 |
Total |
493 |
507 |
Cum frecvențele
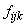 teoretice
sunt
teoretice
sunt 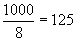 și
și
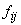 teoretice
sunt
teoretice
sunt 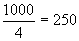 , valoarea
testului
, valoarea
testului 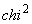 este:
este:
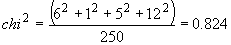 , în cazul
frecvenței
, în cazul
frecvenței 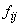 (3 grade
de libertate)
(3 grade
de libertate)
respectiv,
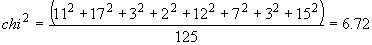 (7 grade
de libertate), în cazul frecvențelor
(7 grade
de libertate), în cazul frecvențelor 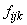 .
.
Ca să
respingem ipoteza independenței cu certitudine 95% că nu o să respingem o ipoteză
adevărată, ne-ar trebui ca 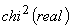 să fie
mai mare decât
să fie
mai mare decât 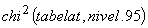 care,
pentru 3 grade de libertate, este 7.815 iar pentru 7, este 14.067 (vezi de exemplu
[66]). Deci nu putem respinge ipoteza independenței.
Putem să o acceptăm. Nu știu. E o chestiune de bun simț că aruncările nu se
influențează una pe alta; tendința de realizare rămâne aceeași atât a stemei,
cât și a banului, indiferent de aruncarea precedentă. Aceasta nu este, bineînțeles,
o demonstrație. Noi am decis că este foarte potrivit să acceptăm ipoteza
care,
pentru 3 grade de libertate, este 7.815 iar pentru 7, este 14.067 (vezi de exemplu
[66]). Deci nu putem respinge ipoteza independenței.
Putem să o acceptăm. Nu știu. E o chestiune de bun simț că aruncările nu se
influențează una pe alta; tendința de realizare rămâne aceeași atât a stemei,
cât și a banului, indiferent de aruncarea precedentă. Aceasta nu este, bineînțeles,
o demonstrație. Noi am decis că este foarte potrivit să acceptăm ipoteza
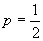 .
.
În figura de mai jos este prezentată evoluția frecvenței relative cumulate.
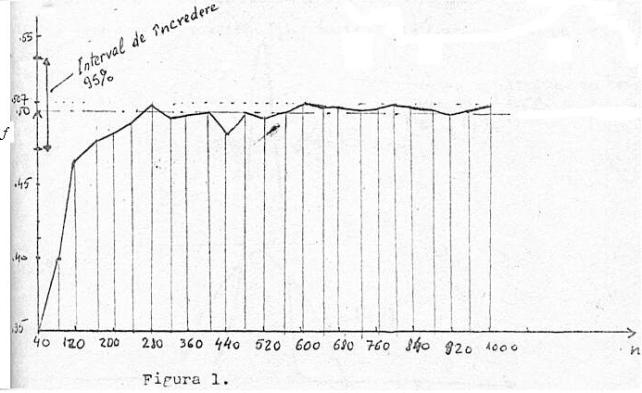
Apliând
calculele de la pag. 127 (97 ???) se găsește că intervalul 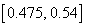 este un
interval de încredere la nivel de semnificație 95% pentru adevăratul p.
este un
interval de încredere la nivel de semnificație 95% pentru adevăratul p.
Să arătăm acum și punctul de vedere Bayesian, susținut de Savage ([53]). Să presupunem că
nici un subiect nu are nici o idee
ce valoare să atribuie probabilității apariției stemei. Tot ce știe este că
banul nu poate cădea pe o muchie. El are o densitate apriori a convingerii sale
asupra lui 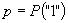 , notată
, notată
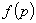 . Funcția
. Funcția
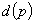 se presupune
continuă și
se presupune
continuă și 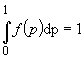 . Să admitem
(ceea ce este foarte nenatural, dar nu are importanță) că
. Să admitem
(ceea ce este foarte nenatural, dar nu are importanță) că 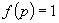 ; adică
pentru subiectul nostru toate valorile p sunt la fel de incerte.
; adică
pentru subiectul nostru toate valorile p sunt la fel de incerte.
După efectuarea experimentului descris mai sus, din motive de coerență (teorema Bayes), densitatea aposteriori a gradului său de încredere asupra lui p este
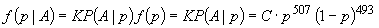 ,
,
unde A este evenimentul care consta în apariția a 507 de steme și K, C sunt constante alese astfel
încât 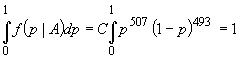 . Un calcul
elementar arată că
. Un calcul
elementar arată că 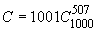 . Să notăm
. Să notăm
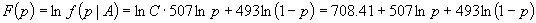
 |
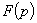 și
și
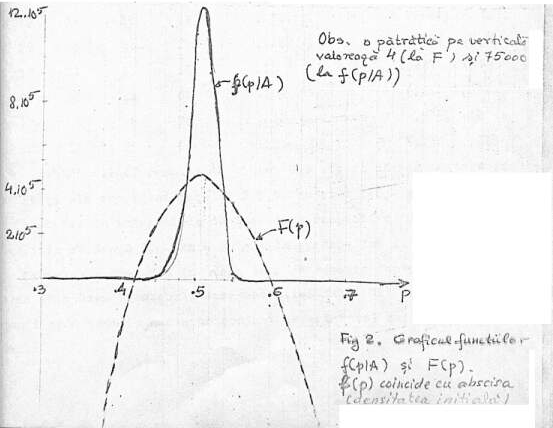
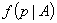 . Se observă
că graficul densității aposteriori arată clar că, dacă subiectul este coerent,
credința lui trebuie să fie foarte mare că
. Se observă
că graficul densității aposteriori arată clar că, dacă subiectul este coerent,
credința lui trebuie să fie foarte mare că 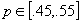 .
. Deoarece cele două figuri sunt foarte distorsionate (din motive tehnice evidente), vom arăta comportarea celor două funcții în tabelul următor, pentru a vedea ce numere apar:
|
p |
.1 |
.2 |
.3 |
.4 |
.45 |
.5 |
.507(max) |
.52 |
.55 |
|
|
0 |
0 |
0 |
.00001 |
1863.2 |
1167321 |
1279425.6 |
908908 |
30946 |
|
|
-504 |
-221 |
-79.3 |
-9.2 |
7.53 |
13.97 |
14.06 |
13.72 |
10.34 |
|
p |
.58 |
.6 |
.7 |
.8 |
.9 |
|
|
26.1 |
.02 |
0 |
0 |
0 |
|
|
3.26 |
-3.31 |
-71 |
-182 |
-491 |
EXEMPLUL 2.
Zarul cu care s-a făcut eprimentul din Anexa următoare a fost aruncat de 360 de ori, în trei serii de câte 120 din următoarea poziție fixată: fața 6 în sus, fața 5 înspre experimentator, înălțimea de la care i s-a dat drumul să cadă liber a fost de 5 cm.
Rezultatele sunt prezentate în tabelul de mai jos
|
I |
II |
III |
Total |
Frecvențe relative |
Int. de încredere 5% |
|
|
1 |
19 |
14 |
16 |
49 |
.136 |
|
|
2 |
29 |
43 |
46 |
118 |
.328 |
|
|
3 |
12 |
11 |
13 |
36 |
.10 |
|
|
4 |
20 |
30 |
11 |
61 |
.169 |
|
|
5 |
10 |
9 |
9 |
28 |
.078 |
|
|
6 |
30 |
13 |
25 |
68 |
.189 |
|
Cum
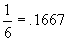 rezultă
că suntem 95% siguri că adevăratele probabilități ale apariției fețelor 2, 3,
5 nu sunt
rezultă
că suntem 95% siguri că adevăratele probabilități ale apariției fețelor 2, 3,
5 nu sunt 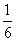 - altfel
- altfel
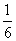 trebuia
să fie în intervalele de încredere respective. Cel mai mult a ieșit în evidență
2, care a apărut în aproape 30% din cazuri.
trebuia
să fie în intervalele de încredere respective. Cel mai mult a ieșit în evidență
2, care a apărut în aproape 30% din cazuri.
Exemplul a fost dat în ideea de a se remarca faptul că nu are sens să spunem Probabilitatea apariției feței 2 la zar decât atunci când avem în minte un context experimental suficient de precizat.