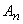 sunt independente
și având aceeași probabilitate p,
sunt independente
și având aceeași probabilitate p, 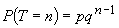 , unde
, unde
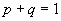 și T
este timpul de așteptare până la realizarea unuia
din evenimentele
și T
este timpul de așteptare până la realizarea unuia
din evenimentele 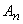 . În cazul
zarului perfect ar trebui, deci, ca
. În cazul
zarului perfect ar trebui, deci, ca 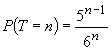 .
.ANEXA 2. Studiul unui exemplu de așteptare
Am aruncat
un zar de câteva mii de ori urmărind să observ de câte aruncări este nevoie
pentru a obține un 6. Variabila aleatoare studiată a fost timpul de așteptare
până la apariția unui 6. Calcule elementare arată că dacă 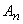 sunt independente
și având aceeași probabilitate p,
sunt independente
și având aceeași probabilitate p, 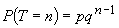 , unde
, unde
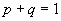 și T
este timpul de așteptare până la realizarea unuia
din evenimentele
și T
este timpul de așteptare până la realizarea unuia
din evenimentele 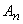 . În cazul
zarului perfect ar trebui, deci, ca
. În cazul
zarului perfect ar trebui, deci, ca 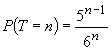 .
.
Experimentele au fost împărțite în serii de câte 200 de experiențe. Rezultatele sunt prezentate în tabelele de mai jos.
Tabelul 1. Frecvențe brute în serii de 200 de probe
|
Nr. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
1 |
55 |
46 |
38 |
48 |
34 |
54 |
38 |
37 |
40 |
35 |
42 |
36 |
35 |
34 |
45 |
38 |
|
2 |
22 |
29 |
22 |
36 |
33 |
32 |
28 |
35 |
30 |
36 |
29 |
27 |
33 |
40 |
36 |
42 |
|
3 |
20 |
33 |
31 |
31 |
35 |
24 |
25 |
32 |
24 |
21 |
17 |
32 |
26 |
34 |
17 |
24 |
|
4 |
16 |
19 |
27 |
21 |
25 |
19 |
24 |
21 |
17 |
28 |
23 |
23 |
14 |
24 |
15 |
20 |
|
5 |
19 |
19 |
18 |
18 |
16 |
16 |
15 |
16 |
20 |
12 |
18 |
18 |
25 |
11 |
20 |
14 |
|
6 |
17 |
9 |
17 |
9 |
12 |
10 |
11 |
17 |
12 |
17 |
16 |
13 |
11 |
12 |
12 |
9 |
|
7 |
11 |
12 |
10 |
7 |
8 |
5 |
15 |
13 |
11 |
11 |
9 |
10 |
10 |
4 |
9 |
12 |
|
8 |
9 |
7 |
9 |
8 |
5 |
11 |
10 |
5 |
9 |
9 |
12 |
9 |
6 |
6 |
11 |
4 |
|
9 |
8 |
3 |
5 |
4 |
5 |
7 |
5 |
4 |
10 |
4 |
5 |
6 |
7 |
7 |
5 |
9 |
|
10 |
3 |
6 |
4 |
6 |
7 |
5 |
7 |
4 |
10 |
5 |
5 |
6 |
7 |
7 |
7 |
7 |
|
11 |
6 |
4 |
5 |
2 |
3 |
5 |
7 |
6 |
4 |
4 |
8 |
2 |
6 |
4 |
8 |
4 |
|
12 |
5 |
3 |
2 |
3 |
6 |
2 |
5 |
1 |
2 |
5 |
2 |
5 |
2 |
2 |
2 |
3 |
|
13 |
2 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
3 |
0 |
3 |
1 |
3 |
3 |
5 |
0 |
|
14 |
4 |
0 |
2 |
1 |
2 |
3 |
2 |
3 |
2 |
2 |
1 |
1 |
5 |
2 |
0 |
1 |
|
15 |
4 |
2 |
2 |
0 |
3 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
1 |
4 |
3 |
0 |
|
16 |
2 |
2 |
2 |
0 |
3 |
2 |
2 |
3 |
0 |
1 |
1 |
4 |
4 |
1 |
1 |
0 |
|
17 |
2 |
1 |
2 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
2 |
|
18 |
0 |
0 |
1 |
2 |
0 |
2 |
0 |
0 |
1 |
2 |
0 |
1 |
1 |
0 |
0 |
3 |
|
19 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
20 |
5 |
4 |
0 |
1 |
2 |
3 |
5 |
4 |
2 |
2 |
5 |
5 |
2 |
5 |
2 |
7 |
și peste
Tabelul 2. Frecvențe cumulate; primul rând arată la câte probe sunt calculate frecvențele.
|
Nr. |
200 |
400 |
600 |
800 |
1000 |
1200 |
1600 |
2000 |
2400 |
2800 |
3200 |
frecv. teoretice pt. |
|
1 |
55 |
101 |
139 |
188 |
222 |
276 |
351 |
428 |
506 |
575 |
658 |
672 |
|
2 |
22 |
51 |
73 |
109 |
142 |
174 |
237 |
303 |
359 |
432 |
510 |
531 |
|
3 |
20 |
53 |
84 |
115 |
150 |
174 |
231 |
276 |
325 |
385 |
426 |
419 |
|
4 |
16 |
35 |
62 |
83 |
108 |
127 |
172 |
217 |
263 |
301 |
336 |
331 |
|
5 |
19 |
38 |
56 |
74 |
90 |
106 |
137 |
169 |
205 |
241 |
275 |
262 |
|
6 |
17 |
26 |
43 |
52 |
64 |
74 |
102 |
131 |
160 |
183 |
204 |
206 |
|
7 |
11 |
23 |
33 |
40 |
48 |
53 |
81 |
103 |
122 |
136 |
157 |
163 |
|
8 |
9 |
16 |
25 |
33 |
38 |
49 |
64 |
82 |
103 |
115 |
130 |
129 |
|
9 |
8 |
11 |
16 |
20 |
25 |
32 |
41 |
55 |
66 |
80 |
94 |
102 |
|
10 |
3 |
9 |
13 |
19 |
26 |
31 |
42 |
57 |
68 |
82 |
96 |
81 |
|
11 |
6 |
10 |
15 |
17 |
20 |
25 |
38 |
46 |
56 |
66 |
78 |
64 |
|
12 |
5 |
8 |
10 |
13 |
19 |
21 |
27 |
34 |
41 |
45 |
50 |
50 |
|
13 |
2 |
3 |
5 |
7 |
8 |
9 |
13 |
16 |
20 |
26 |
31 |
40 |
|
14 |
4 |
4 |
6 |
7 |
9 |
12 |
17 |
21 |
23 |
30 |
31 |
31 |
|
15 |
4 |
6 |
8 |
8 |
11 |
12 |
14 |
18 |
21 |
26 |
29 |
25 |
|
16 |
2 |
4 |
6 |
6 |
9 |
11 |
16 |
17 |
22 |
26 |
27 |
20 |
|
17 |
2 |
3 |
5 |
6 |
7 |
8 |
9 |
11 |
12 |
13 |
16 |
15 |
|
18 |
0 |
0 |
2 |
4 |
4 |
6 |
6 |
9 |
10 |
11 |
14 |
12 |
|
19 |
0 |
0 |
0 |
2 |
2 |
2 |
3 |
7 |
7 |
8 |
10 |
10 |
|
20 |
5 |
9 |
9 |
9 |
11 |
14 |
23 |
27 |
37 |
44 |
53 |
49 |
și peste
Notând
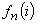 frecvențele
relative cumulate (la n probe) ca timpul de așteptare să fie exact i,
atunci este clar că
frecvențele
relative cumulate (la n probe) ca timpul de așteptare să fie exact i,
atunci este clar că 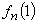 este un
estimator pentru p = probabilitatea apariției unui 6. Iată evoluția acestei
frecvențe relative pentru n dat în tabelul 2 (adică n = 200, 400,
,3200):
este un
estimator pentru p = probabilitatea apariției unui 6. Iată evoluția acestei
frecvențe relative pentru n dat în tabelul 2 (adică n = 200, 400,
,3200):
.275, .252, .232, .235, .222, .230, .219, .214, .211, .205, .2056.
Am preferat
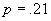 și nu
.205 deoarece frecvențele au fost toate deasupra lui .205; trebuie aleasă ca
probabilitate o frecvență în jurul căreia oscilează celelalte.
și nu
.205 deoarece frecvențele au fost toate deasupra lui .205; trebuie aleasă ca
probabilitate o frecvență în jurul căreia oscilează celelalte.
Calculând
testul 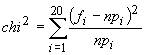 a rezultat
un
a rezultat
un 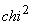 calculat
de 14.7 care nu este suficient pentru a infirma ipoteza că
calculat
de 14.7 care nu este suficient pentru a infirma ipoteza că 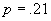 (la 19
grade de libertate câte avem, ar trebui un
(la 19
grade de libertate câte avem, ar trebui un 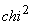
mai mare decât 30.1 pentru a respinge ipoteza cu probabilitate de eroare mai mică decât 5%.
 Dacă am fi ales
Dacă am fi ales 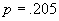 , abaterea
de la curba teoretică ar fi fost și mai mică (
, abaterea
de la curba teoretică ar fi fost și mai mică ( 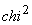 =12.83)
dar am preferat
=12.83)
dar am preferat 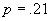 din motive
empirice: o valoare mai de mijloc a frecvenei relative este, probabil, mai
apropiată de adevărata probabilitate (!).
din motive
empirice: o valoare mai de mijloc a frecvenei relative este, probabil, mai
apropiată de adevărata probabilitate (!).
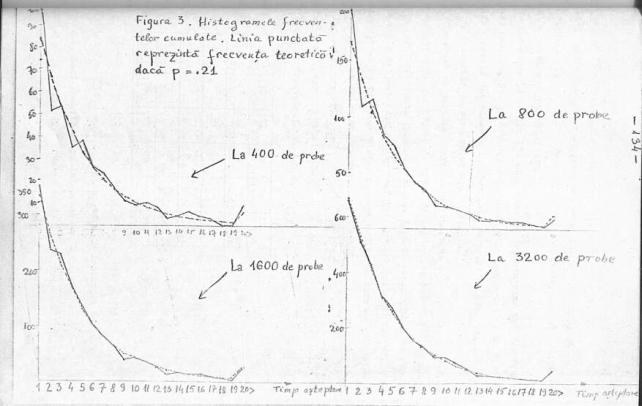
În figura
de pe pagina [134???] este arătată
evoluția frecvențelor relative cumulate după 400, 800, 1600 și 3200 de experimente. Am putea decide
de aici că modelul teoretic evenimente independente cu 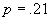 se potrivește
aproape perfect. Lucrurile nu stau chiar așa de simplu.
se potrivește
aproape perfect. Lucrurile nu stau chiar așa de simplu.
Am încercat să varific ipoteza independenței (de fapt, aici ar fi mai adecvată noțiunea lui Popper de falsificare). Din cele 16365 de aruncări cu zarul efectuate (pentru a obține 3200 de experimente) am reținut ultima serie de 3065 (din motive tehnice: numărătorile au fost făcute manual; altfel aș fi putut studia întreaga serie) pe care am studiat-o mai amănunțit. Am calculat frecvențele
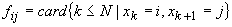 ,
,
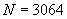 ,
,
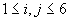
pe care le-am trecut în tabelul 3.
TABELUL 3. Frecvențele 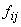 și
și
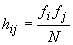
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
1 |
117 -8 125 |
103 11 92 |
123 24 93 |
79 12 87 |
78 -16 94 |
118 -3 121 |
618 |
|
2 |
100 8 92 |
67 -11 68 |
82 9 73 |
54 -10 64 |
75 6 69 |
78 -12 90 |
456 |
|
3 |
97 -2 99 |
87 6 73 |
67 -12 79 |
67 -2 69 |
74 -1 75 |
101 4 97 |
493 |
|
4 |
80 -7 87 |
53 -11 64 |
53 -16 69 |
74 14 60 |
71 6 65 |
99 8 91 |
430 |
|
5 |
101 7 94 |
70 1 69 |
75 0 75 |
67 2 65 |
78 7 71 |
74 -17 91 |
465 |
|
6 |
123 2 121 |
76 -14 90 |
93 -4 97 |
89 -2 91 |
89 -2 91 |
132 14 118 |
602 |
|
|
618 |
456 |
493 |
430 |
465 |
602 |
3064 (total) |
Să notăm 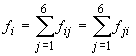 și
și
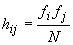 (rotunjit
la parte întreagă). Atunci, dacă probele ar fi independente, ar trebui ca
(rotunjit
la parte întreagă). Atunci, dacă probele ar fi independente, ar trebui ca
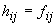 aproximativ;
dacă în loc de frecvențe am fi lucrat cu probabilități, ar fi trebuit ca
aproximativ;
dacă în loc de frecvențe am fi lucrat cu probabilități, ar fi trebuit ca
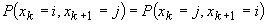 ???. În
colțul din dreapta jos al celulelor (i, j) am notat valoarea lui
???. În
colțul din dreapta jos al celulelor (i, j) am notat valoarea lui
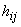 , iar în
colțul din stânga jos, abaterea de la aceste valori semiteoretice,
, iar în
colțul din stânga jos, abaterea de la aceste valori semiteoretice, 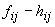 .
.
Deși la o simplă inspectare a acestor valori s-ar părea că abaterile nu sunt prea mari, și că nu avem motive serioase să respingem ipoteza independenței, valoarea indicatorului
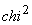
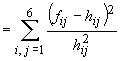
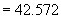
Valoarea
tabelată a aceluiași indicator pentru respingerea ipotezei la nivel de semnificație
5% și 30 grade de libertate ( 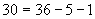 : avem
36 de căsuțe și 5 legături independente între ele de tipul
: avem
36 de căsuțe și 5 legături independente între ele de tipul 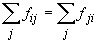 ) este
ceva mai mare 43.773, dar la nivel 10%
) este
ceva mai mare 43.773, dar la nivel 10% 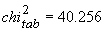 .
.
Înseamnă că ipoteza independenței trebuie respinsă (cu risc între 5% și 10% de a comite o eroare). Există o explicație intuitivă a faptului că aruncările nu au fost independente: la ultimele probe, nu mai amestecam zarul în mână, ci îl luam de pe masă și îl lăsam să se rostogolească din palmă în cădere liberă de la o înălțime de 10 15 centimetri. De aceea probabil că a apărut o dependență markoviană între aruncări.
Se știe
că numerele 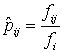 reprezintă
o estimare a probabilităților de trecere ale lanțului. În cazul de față
reprezintă
o estimare a probabilităților de trecere ale lanțului. În cazul de față
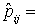

Se observă
că dependența markoviană este destul de slabă: doar cinci dintre numerele
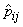 se abat
de la
se abat
de la 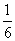 cu mai
mult de .05 (
cu mai
mult de .05 ( 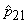 ,
,
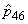 ,
,
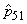 și
și
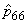 ). Este
de așteptat, deci, ca rezltatul comportării acestui lanț Markov să nu difere
prea mult de cazul în care variabilele
). Este
de așteptat, deci, ca rezltatul comportării acestui lanț Markov să nu difere
prea mult de cazul în care variabilele 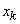 ar fi
independente și identic repartizate. Acest lucru ar explica de ce modelul inițial
s-a potrivit așa de bine.
ar fi
independente și identic repartizate. Acest lucru ar explica de ce modelul inițial
s-a potrivit așa de bine.
În matricea din Tabelul 3, să considerăm că nu ne interesează decât dacă rezultatul aruncării a fost 6 sau non-6. Pe 6 să îl renotăm cu 1 (succes) și pe non-6 cu 0 (eșec). Atunci tabelul frecvențelor devine:
Tabelul 4. Același ca Tabelul 3, dar rezultatele 1, 2, 3, 4, 5, 6 se cumulează sub eticheta 0 iar 6 este renotat 1.
|
0 |
1 |
||
|
0 |
1992 14 1978 |
470 14 484 |
2462 |
|
1 |
470 -14 484 |
132 14 118 |
602 |
|
Total |
2462 |
602 |
3084 |
Convențiile
sunt aceleași ca în Tabelul 3: în stânga jos sunt abaterile de la valorile
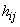 care apar
în colțul din dreapta jos.
care apar
în colțul din dreapta jos.
Acum
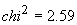 , adică
insuficient pentru a respinge ipoteza că probele sunt independente. Ori, în
cazul experimentului de așteptare efectuat nu interesează decât 6
și non-6, adică 0 și 1. De aceea ipoteza independenței a fost, totuși, adecvată.
, adică
insuficient pentru a respinge ipoteza că probele sunt independente. Ori, în
cazul experimentului de așteptare efectuat nu interesează decât 6
și non-6, adică 0 și 1. De aceea ipoteza independenței a fost, totuși, adecvată.
Un interval
de încredere de nivel 95% pentru adevărata probabilitate a apariției feței 6
este 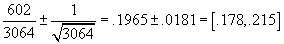 . Atât
valorile .21 și .205 gasite prin metoda cealaltă, de la pag. 133 (
. Atât
valorile .21 și .205 gasite prin metoda cealaltă, de la pag. 133 ( 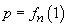 ) sunt
acceptabile.
) sunt
acceptabile.
Să luăm
acum în considerație modelul markovian. Lucrurile nu se complică prea mult.
Considerăm că noile variabile aleatoare 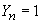
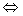
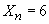 și
și
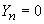 în rest,
formează un lanț Markov omogen și staționar (adică
în rest,
formează un lanț Markov omogen și staționar (adică 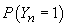 nu depinde
de n). Matricea de trecere
nu depinde
de n). Matricea de trecere 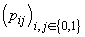 o estimăm
din Tabelul 4. Atunci
o estimăm
din Tabelul 4. Atunci 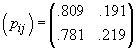 . Trebuie
să calculăm
. Trebuie
să calculăm 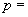
 . Din ipoteza
de staționaritate,
. Din ipoteza
de staționaritate, 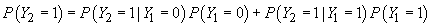 sau
sau
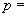
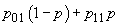 ,de unde
se scoate imediat
,de unde
se scoate imediat 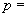
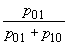 sau, în
cazul nostru
sau, în
cazul nostru 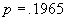 .
.
Introducem
acum variabila aleatoare T =
timpul de așteptare până la apariția succesului, 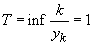 . Un calcul
elementar (condiționări repetate) arată că
. Un calcul
elementar (condiționări repetate) arată că 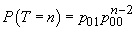 dacă
dacă
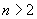 și
și
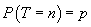 . La 3200
de probe, frecvențele apropiate vor fi:
. La 3200
de probe, frecvențele apropiate vor fi:
T |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
f |
629 |
491 |
397 |
321 |
260 |
210 |
170 |
138 |
111 |
90 |
73 |
59 |
48 |
39 |
31 |
25 |
20 |
|
f (real) |
658 |
510 |
426 |
336 |
275 |
204 |
157 |
130 |
94 |
96 |
78 |
50 |
31 |
31 |
29 |
27 |
16 |
Care, în mod paradoxal, sunt mai proaste decât cele obținute prin modelul naiv i.i.d !