ANEXA 3. Metoda funcțiilor arbitrare
În [46],
1912, §92 și §93, Poincaré și-a pus problema explicării
echiprobabilității care apare în anumite jocuri de noroc, cum ar fi ruleta.
Ideea sa a fost reluată și comentată apoi de Reichenbach (1935), Frechet (1952)
și, mai ales, Hincin (1953). În ultima lucrare se consideră că pe baza acestei
metode posibilitatea principală a unei prevederi științifice obiective a stabilității
și valorii numerice ale frecvențelor reale este ferm stabilită. Pe viitor, lărgirea
sferei de aplicații ale ei va putea întâmpina în fond, numai dificultăți matematice
de ordin tehnic, care în zilele noastre sunt, este drept, destul de importante
(citat din [3], pag. 245).
Înainte
de a comenta acest citat să vedem despre ce este vorba. Se știe că ruleta este,
în esență, o roată împărțită în 36 de sectoare circulare de câte 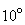 fiecare
(sau
fiecare
(sau 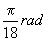 ). Sectoarele
sunt, alternativ, roșii și negre. Dacă ruleta se oprește pe negru, să spunem
că avem un succes; în caz contrar, avem un eșec. Ne propunem să calculăm probabilitățile
). Sectoarele
sunt, alternativ, roșii și negre. Dacă ruleta se oprește pe negru, să spunem
că avem un succes; în caz contrar, avem un eșec. Ne propunem să calculăm probabilitățile
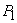 și
și
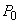 ale succesului
(respectiv eșecului). Poincaré presupune, într-o primă aproximație, că putem
neglija frecarea: roata capătă o viteză inițială de rotație
ale succesului
(respectiv eșecului). Poincaré presupune, într-o primă aproximație, că putem
neglija frecarea: roata capătă o viteză inițială de rotație 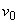 pe care
și-o menține până când este oprită brusc după T secunde. Unghiul
parcurs este egal, evident, cu
pe care
și-o menține până când este oprită brusc după T secunde. Unghiul
parcurs este egal, evident, cu 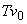 . Să presupunem
că
. Să presupunem
că 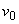 este o
variabilă aleatoare continuă, având o densitate de repartiție f despre
care nu mai este nevoie să presupunem nimic. Atunci densitatea de repartiție
a unghiului
este o
variabilă aleatoare continuă, având o densitate de repartiție f despre
care nu mai este nevoie să presupunem nimic. Atunci densitatea de repartiție
a unghiului 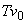 este
este
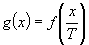 . Admițând
că ruleta pleacă tot timpul din aceeași poziție și că primul sector, în sens
trigonometric, care apare este cel roșu, avem (notând
. Admițând
că ruleta pleacă tot timpul din aceeași poziție și că primul sector, în sens
trigonometric, care apare este cel roșu, avem (notând 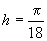 ):
):
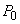
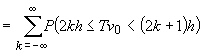
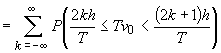
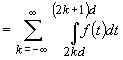 ,
,
unde 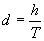 .
.
Analog
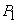
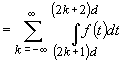
Rezultă:
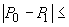
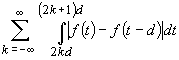
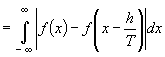
Se știe însă (vezi de exemplu [2], pag. 417, pr.8) că dacă 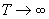 , ultima
cantitate converge la 0.
, ultima
cantitate converge la 0.
Să considerăm
acum un model ceva mai apropiat de realitate. Viteza inițială, 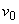 este uniform
frânată de o forță de frecare. Deci
este uniform
frânată de o forță de frecare. Deci 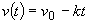 , unde
k este un coeficient de frecare. Presupunem că roata este lăsată până
se oprește singură. Acest lucru se va întâmpla când
, unde
k este un coeficient de frecare. Presupunem că roata este lăsată până
se oprește singură. Acest lucru se va întâmpla când 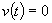 , deci
la timpul
, deci
la timpul 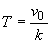 . Unghiul
parcurs după acest timp va fi egal cu
. Unghiul
parcurs după acest timp va fi egal cu 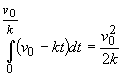 . Notând
acest unghi cu A, avem
. Notând
acest unghi cu A, avem
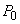
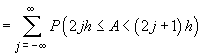
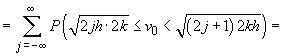
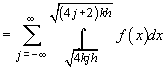
și, analog, 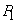
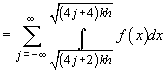 .
.
Notând
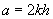 , rezultă:
, rezultă:
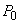 -
-
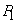
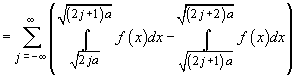 .
.
Vom arăta
că dacă coeficientul de frecare tinde spre 0 (roata este bine unsă), atunci
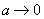
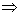
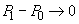 . Demonstrația
se va baza pe următorul rezultat:
. Demonstrația
se va baza pe următorul rezultat:
Lemă.
1. Fie 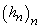 un șir
monoton de numere pozitive. Atunci:
un șir
monoton de numere pozitive. Atunci:
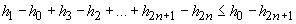 .
.
2. Fie 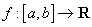 o funcție
continuă și
o funcție
continuă și 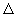
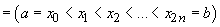 o diviziune
a intervalului
o diviziune
a intervalului 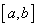 . Fie
. Fie
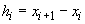 și
și
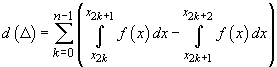 .
.
Atunci, dacă șirul 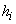 este monoton
și
este monoton
și 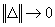 , rezultă
, rezultă
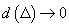 .
.
3. Fie 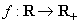 o densitate
de probabilitate și
o densitate
de probabilitate și 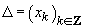 o diviziune
a lui R. Fie
o diviziune
a lui R. Fie 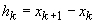 și
și
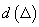 cu aceeași
definiție ca la 2., dar suma se extinde pentru toți
cu aceeași
definiție ca la 2., dar suma se extinde pentru toți 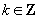 . Dacă
presupunem că
. Dacă
presupunem că 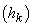 este un
șir monoton sau unimodal (crește până la un
este un
șir monoton sau unimodal (crește până la un 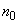 și apoi
scade), rămâne valabilă concluzia de la punctul 2.
și apoi
scade), rămâne valabilă concluzia de la punctul 2.
Demonstrație.
1. Să admitem că 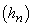 este crescător.
Atunci
este crescător.
Atunci
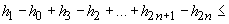
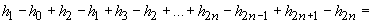
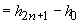 (termenii
se reduc doi câte doi)
(termenii
se reduc doi câte doi)
2. Fie 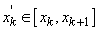 astfel
încât
astfel
încât 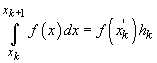 (teorema
Lagrange !). Fie
(teorema
Lagrange !). Fie 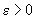 cu proprietatea
că
cu proprietatea
că 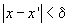
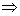
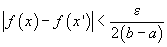 ( f
este uniform continuă !) și
( f
este uniform continuă !) și 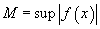 , norma
uniformă a lui f.
, norma
uniformă a lui f.
Atunci
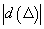
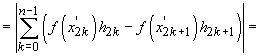
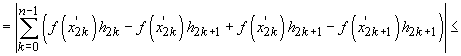
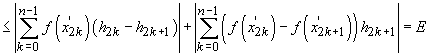
Să presupunem,
ca să facem o alegere, că șirul 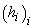 este descrescător
. În această situație norma diviziunii este
este descrescător
. În această situație norma diviziunii este 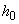 (altfel
ar fi
(altfel
ar fi 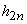 ) și, dacă
presupunem că
) și, dacă
presupunem că 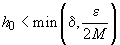 , expresia
E este mai mică decât
, expresia
E este mai mică decât 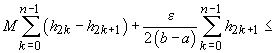
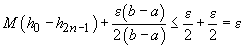 . Cum
. Cum
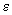 este arbitrar,
demonstrația este încheiată.
este arbitrar,
demonstrația este încheiată.
Să remarcăm
că, dacă familia 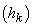 era unimodală,
demonstrația nu se schimba prea mult. Estimarea 1. care a fost esențială devenea:
era unimodală,
demonstrația nu se schimba prea mult. Estimarea 1. care a fost esențială devenea:
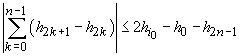 , unde
, unde
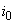 este acel
indice pentru care segmentul
este acel
indice pentru care segmentul 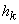 are lungime
maximă.
are lungime
maximă.
3. Se știe că pentru orice funcție
măsurabilă Lebesgue și cu proprietatea că 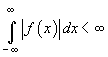 și pentru
orice
și pentru
orice 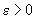 există
o altă funcție continuă g care este nulă în afara unui interval
există
o altă funcție continuă g care este nulă în afara unui interval
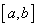 și cu
proprietatea că
și cu
proprietatea că 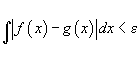 . După
majorarea
. După
majorarea
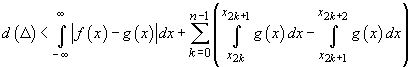 ,
,
unde diviziunea a fost renumerotată, cu adăugarea eventuală
a punctelor a și b, restul devine evident. QED.
În cazul
nostru, dacă coefeicientul de frecare 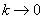
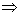
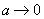
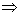
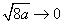 ; dar ultima
cantitate este exact norma diviziunii dată de punctele
; dar ultima
cantitate este exact norma diviziunii dată de punctele 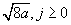 , care
apare în modelul propus. Deoarece, în plus
, care
apare în modelul propus. Deoarece, în plus 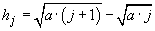 formează
un șir descrescător, rezultă că suntem în condițiile Lemei demonstrate (3.)
și deci
formează
un șir descrescător, rezultă că suntem în condițiile Lemei demonstrate (3.)
și deci 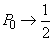 .
.
Ce se
poate spune despre valoarea explicativă a acestei metode ?
Am demonstrat
că 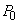 și
și
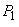 tind spre
tind spre
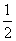 dacă T
tinde la
dacă T
tinde la 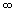 sau coefeicientul
de frecare tinde la 0, ceea ce spune cam același lucru: roata trebuie lăsată
să se învârtească cât mai mult. Dar în ce măsură explică aceasta echiprobabilitatea
rezultatelor ruletei ? Dacă abaterea de la
sau coefeicientul
de frecare tinde la 0, ceea ce spune cam același lucru: roata trebuie lăsată
să se învârtească cât mai mult. Dar în ce măsură explică aceasta echiprobabilitatea
rezultatelor ruletei ? Dacă abaterea de la 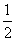 rămâne
foarte mare până când T este, de exemplu, de ordinul secolelor, explicația
devine, cu bunăvoință apreciind, iluzorie. În definitiv, am căzut în aceeași
capcană ca von Mises: postulăm relevanța unei limite la un experiment real.
Pentru fiecare T, în cadrul modelului simplificat al lui Poincaré, ne putem
imagina o repartiție a vitezei inițiale pe care crupierul o imprimă roții care
să aibă și densitatea continuă, dar să ne facă figura că
rămâne
foarte mare până când T este, de exemplu, de ordinul secolelor, explicația
devine, cu bunăvoință apreciind, iluzorie. În definitiv, am căzut în aceeași
capcană ca von Mises: postulăm relevanța unei limite la un experiment real.
Pentru fiecare T, în cadrul modelului simplificat al lui Poincaré, ne putem
imagina o repartiție a vitezei inițiale pe care crupierul o imprimă roții care
să aibă și densitatea continuă, dar să ne facă figura că 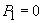 și
și
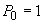 .
.
În al
doilea rând, și acest lucru este poate mai important, am încercat să explicăm
o ipoteză probabilistă prin alta, de asemenea probabilistă. S-ar părea că am
împins problema undeva în spate, într-un plan mai profund și că explicăm o probabilitate
testabilă empiric prin alta neverificabilă. Oare chiar nu se poate reduce o
probabilitate la altceva ? Reichenbach consideră, totuși, în /49/ că metoda
furnizează o explicație e echiprobabilității deoarece am demonstrat ceva tare
din ceva mai slab. Se pare că nu l-a deranjat trecerea la limită.
Pentru
ca o trecere la limită să aibă cât de cât un sens empiric ar trebui să spunem
ceva și despre viteza de convergență la limita respectivă. Ce ipoteze suplimentare
să mai introducem pentru aceasta ? ne vom situa în cazul modelului lui Poincaré,
căci altfel estimările devin dificile.
Să admitem
că densitatea f este continuă și concentrată pe un interval închis
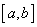 cu
cu
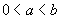 . Nu pare
o restricție nenaturală: în natură, majoritatea fenomenelor sunt, la o primă
aproximatie continui și este plauzibil de presupus că
. Nu pare
o restricție nenaturală: în natură, majoritatea fenomenelor sunt, la o primă
aproximatie continui și este plauzibil de presupus că 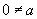 (dacă
viteza de rotație a roții este prea mică (de ordinul miimilor de grad pe secundă)
e normal să cerem alt joc, bănuind pe crupier de cârdășie cu banca și intenții
necinstite) și că există o limită fizică a vitezei de rotație pe care o poate
imprima ruletei. Până acum nu am avansat nici un pas pe drumul estimării vitezei
de convergență. Dar să admitem că cunoaștem modulul de continuitate al densității
f (adică, pentru fiecare
(dacă
viteza de rotație a roții este prea mică (de ordinul miimilor de grad pe secundă)
e normal să cerem alt joc, bănuind pe crupier de cârdășie cu banca și intenții
necinstite) și că există o limită fizică a vitezei de rotație pe care o poate
imprima ruletei. Până acum nu am avansat nici un pas pe drumul estimării vitezei
de convergență. Dar să admitem că cunoaștem modulul de continuitate al densității
f (adică, pentru fiecare 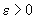 știm să
calculăm
știm să
calculăm 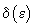 cu proprietatea
că
cu proprietatea
că 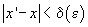
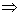
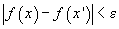 ). Atunci,
deoarece
). Atunci,
deoarece 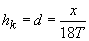 ,
,
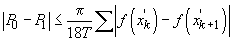 și
și
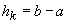 , dacă
vrem ca
, dacă
vrem ca 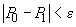 , trebuie
ales
, trebuie
ales 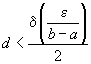 , deoarece
, deoarece
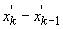 nu poate
depăși valoarea
nu poate
depăși valoarea 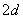 . Deci
. Deci
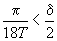 sau
sau
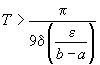 .
.
Să presupunem
acum că f este, în plus unimodală (are un singur maxim) și maximul ei
este M. Atunci este ușor de văzut că 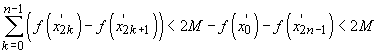 .
.
Rezultă
că 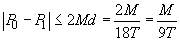 . Dacă
vrem ca această valoare să fie mai mică decât
. Dacă
vrem ca această valoare să fie mai mică decât 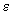 , trebuie
ca
, trebuie
ca 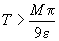 . În cazul
acesta nu mai este nevoie ca f să fie continuă cu suport compact: estimarea
. În cazul
acesta nu mai este nevoie ca f să fie continuă cu suport compact: estimarea
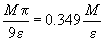 (1) este
valabilă pentru orice densitate f unimodală.
(1) este
valabilă pentru orice densitate f unimodală.
Un caz
particular de funcții al căror modul de continuitate poate fi continuitate sunt
cele Lipschitziene, adică având proprietatea că există o constantă C
astfel ca 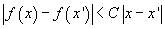 . Dacă
densitatea f este Lipschitziană de modul C, atunci
. Dacă
densitatea f este Lipschitziană de modul C, atunci 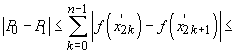
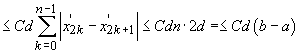 (deoarece
(deoarece
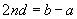 )
)
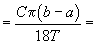
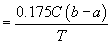 ; deci
(???? pag. 142) ca ultima cantitate să fie mai mică decât
; deci
(???? pag. 142) ca ultima cantitate să fie mai mică decât 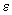 , trebuie
ca
, trebuie
ca 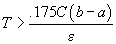 . (2)
. (2)
În particular
acesta este cazul dacă se presupune că densitatea f este derivabilă și
cu derivată mărginită.
Să considerăm
ca divertisment cazul cel mai studiat: 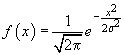 repartiția
normală centrată în 0 și de dispersie
repartiția
normală centrată în 0 și de dispersie 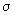 . Calculând
maximul primei derivate găsim
. Calculând
maximul primei derivate găsim 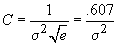 . Cât despre
M, el este egal cu
. Cât despre
M, el este egal cu 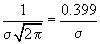 . Folosind
estimarea (1), găsim
. Folosind
estimarea (1), găsim 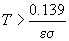 , iar folosind
pe (2) găsim
, iar folosind
pe (2) găsim 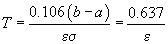 deoarece
putem lua
deoarece
putem lua 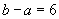 ???
se știe că în cazul unei variabile normale probabilitatea abaterilor cu mai
mult decât
???
se știe că în cazul unei variabile normale probabilitatea abaterilor cu mai
mult decât 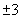 de la
media m este sub 1%. Deși pentru anumite valori ale lui ??? prima
estimare dă rezultate superioare, a doua nu depinde de ???.
de la
media m este sub 1%. Deși pentru anumite valori ale lui ??? prima
estimare dă rezultate superioare, a doua nu depinde de ???.
O altă
problemă celebră în care se poate explica stabilitatea probabilității, remarcată
experimental prin considerente apropiate de cele demai sus este problema
acului lui Buffon (1776). Un ac de lungime 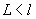 se aruncă
pe o rețea de drepte echidistante situate la distanța l una de alta.
Se cere calcularea probabilității ca acul să intersecteze vreuna din dreptele
rețelei.
se aruncă
pe o rețea de drepte echidistante situate la distanța l una de alta.
Se cere calcularea probabilității ca acul să intersecteze vreuna din dreptele
rețelei.
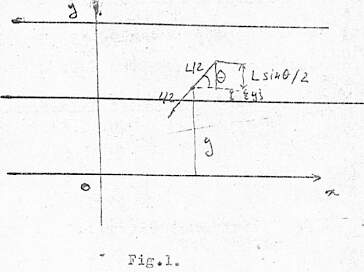 Să considerăm un sistem rectangular de axe xOy
în care dreptele rețelei să fie
Să considerăm un sistem rectangular de axe xOy
în care dreptele rețelei să fie 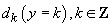 . Putem
răspunde la întrebarea dacă acul intersectează vreuna din dreptele
. Putem
răspunde la întrebarea dacă acul intersectează vreuna din dreptele 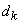 cunoscând
doar doi parametri: ordonata mijlocului acului
cunoscând
doar doi parametri: ordonata mijlocului acului 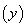 și unghiul
format de ac cu dreptele
și unghiul
format de ac cu dreptele 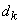 . Atunci,
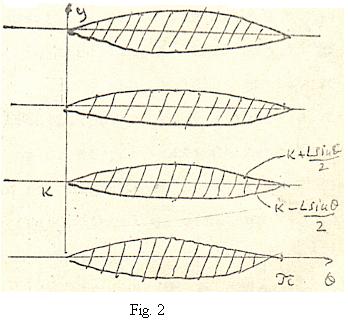
după cum se vede în figura alăturată, acul intersectează una din drepte dacă
și numai dacă
. Atunci,
după cum se vede în figura alăturată, acul intersectează una din drepte dacă
și numai dacă  sau dacă
sau dacă
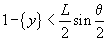 .
.
Să admitem
acum că 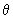 și sunt
variabile aleatoare independente având densitățile de repartiție
și sunt
variabile aleatoare independente având densitățile de repartiție 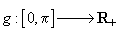 , respectiv
, respectiv
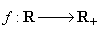 . Probabilitatea
căutată este
. Probabilitatea
căutată este
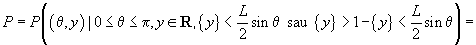
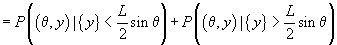
 deoarece cele două evenimente sunt incompatibile
deoarece cele două evenimente sunt incompatibile
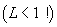 . Remarcând
că aceasta reprezintă probabilitatea suprafețelor hașurate din Fig.2, găsim
că
. Remarcând
că aceasta reprezintă probabilitatea suprafețelor hașurate din Fig.2, găsim
că
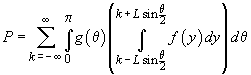 .
.
Acest rezultat nu ne spune prea mult tocmai pentru că
am lucrat în ipoteze prea generale. În teoria probabilităților geometrice se
fac presupuneri suplimentare (vezi, de exemplu /37/)
din care reyultă că atât 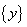 cât și
cât și
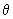 sunt repartizate
uniform pe intervalele
sunt repartizate
uniform pe intervalele 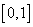 respectiv
respectiv
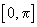 . Cu aceste
. Cu aceste
presupuneri suplimentare este imediat că 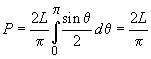 . Dacă
. Dacă
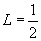 , rezultă
că
, rezultă
că 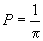 .
.
Acest
rezultat se poate preta la o verificare empirică. Desenăm pe o foaie de carton
paralele echidistante situate la 10 cm una de alta și aruncăm la întâmplare
un ac de 5 cm peste ea. Facem experimentul de multe ori; ar trebui ca inversul
frecvenței relative al cazurilor de intersecție să oscileze pe lângă 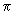 . La o
primă vedere, s-ar părea că nu trebuie să fim prea optimiști asupra rezultatului,
deoarece probabilitatea teoretică a fost obținută în niște ipoteze foarte restrictive.
Nu este așa. Este, din contră, surprinzător că estimările lui
. La o
primă vedere, s-ar părea că nu trebuie să fim prea optimiști asupra rezultatului,
deoarece probabilitatea teoretică a fost obținută în niște ipoteze foarte restrictive.
Nu este așa. Este, din contră, surprinzător că estimările lui 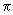 făcute
pe această bază s-au dovedit foarte bune ! Tabelul următor este edificator:
făcute
pe această bază s-au dovedit foarte bune ! Tabelul următor este edificator:
|
Experimentator
|
Nr. aruncări
|
Valoarea estimată pt. 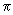
|
|
WOLF, 1850
|
5000
|
3.1596
|
|
SMITH, 1855
|
3204
|
3.1553
|
|
DE MORGAN, 1860
|
600
|
3.137
|
|
FOX, 1884
|
1030
|
3.1595
|
|
LAZZERINI, 1901
|
3408
|
3.1415929 (adevărata valoare este 3.141592654)
|
|
REIN, 1925
|
859
|
3.1795
|
|
GRIDGEMAN, 1960
|
2000
|
3.143
|
(Luat
din /37/, pag. 83). Valoarea nr. 5 (Lazzerini) este chiar suspectă;
făcând abstracție de ea, chiar, intervalul în care au oscilat frecvențele este
sub .05.
Ce se
întâmplă de fapt ? De ce repartițiile reale din natură atribuie ariei hașurate
din Fig. 2 valori atât de apropiate de 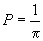 ? Explicația
trebuie să fie că în ipoteze foarte generale asupra lui y partea sa zecimală
tinde să fie uniform repartizată. Ipoteza că
? Explicația
trebuie să fie că în ipoteze foarte generale asupra lui y partea sa zecimală
tinde să fie uniform repartizată. Ipoteza că 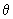 este și
el repartizat uniform pe intervalul
este și
el repartizat uniform pe intervalul 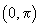 nu mi
se pare atât de nenaturală,căci este de așteptat ca aruncând un ac, unghiul
să nu aibă vreo direcție privilegiată. Din contră, nu este natural să admit
că mijlocul său să nu aibă vreo preferință, o zonă privilegiată în care să cadă.
Dacă arunc o piatră la întâmplare, este sigur că ea va cădea undeva în interioruk
cercului având ca centru locul în care mă aflu și o rază de 100 m). De aceea
este mai natural să admit că y este o variabilă aleatoare repartizată
nu mi
se pare atât de nenaturală,căci este de așteptat ca aruncând un ac, unghiul
să nu aibă vreo direcție privilegiată. Din contră, nu este natural să admit
că mijlocul său să nu aibă vreo preferință, o zonă privilegiată în care să cadă.
Dacă arunc o piatră la întâmplare, este sigur că ea va cădea undeva în interioruk
cercului având ca centru locul în care mă aflu și o rază de 100 m). De aceea
este mai natural să admit că y este o variabilă aleatoare repartizată
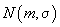 cu o anumită
medie m și dispersie
cu o anumită
medie m și dispersie 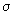 . În acest
caz conjectura se verifică: dacă
. În acest
caz conjectura se verifică: dacă 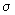 nu este
exagerat de mic,
nu este
exagerat de mic, 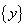 este aproape
uniform repartizat, după cum se arată în următorul rezultat splendid, demonstrat
de S. Teleman (comunicare personală):
este aproape
uniform repartizat, după cum se arată în următorul rezultat splendid, demonstrat
de S. Teleman (comunicare personală):
Teoremă.
Dacă 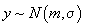 , atunci
, atunci
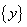 are de
asemenea o repartiție de probabilitate absolut continuă cu densitatea
are de
asemenea o repartiție de probabilitate absolut continuă cu densitatea
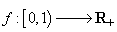 având
proprietatea că
având
proprietatea că 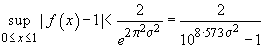
Demonstrație. Avem
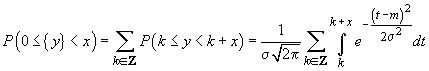 .
.
Deoarece ultima serie este uniform și absolut convergentă,
se poate deriva termen cu termen și găsim densitatea 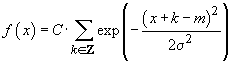 . Funcția
f are sens pentru orice
. Funcția
f are sens pentru orice  ; ea este,
în plus, periodică și are perioadă 1. Am notat
; ea este,
în plus, periodică și are perioadă 1. Am notat 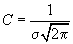 . Să notăm
. Să notăm
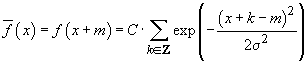 și
și
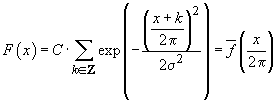 .
.
Evident că dacă vom reuși să demonstrăm estimarea din
enunțul teoremei pentru F va fi suficient deoarece f se obține
din F modificând numai argumentul x.
Funcția
F este periodică și are perioada 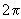 . Fiind
și continuă, se poate dezvolta în serie Fourier
. Fiind
și continuă, se poate dezvolta în serie Fourier 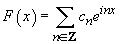 , unde
coeficienții Fourier
, unde
coeficienții Fourier 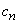 sunt dați
de expresia
sunt dați
de expresia
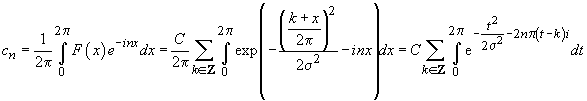

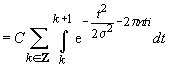
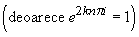
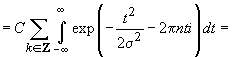
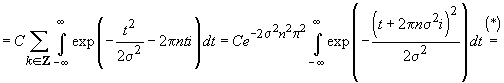 *
*
= 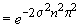 (deoarece
ulrima integrală este egală exact cu
(deoarece
ulrima integrală este egală exact cu 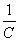 ).
).
De aceea 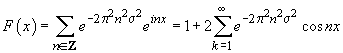 și astfel
și astfel
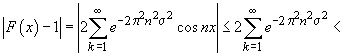
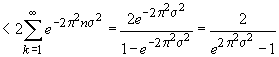 q.e.d.
q.e.d.
Probabil
că acest rezultat se poate extinde și la alte clase de repartiții. Trebuie însă
căutate alte metode, căci în calculul coeficienților s-a folosit esențial forma
exponențială a densității.
Dacă,
de exemplu dispersia 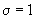 , atunci
abaterea densității f de la 1 este de ordinul lui
, atunci
abaterea densității f de la 1 este de ordinul lui 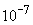 ; pentru
; pentru
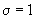 , ea devine
, ea devine
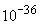 , ceva
extraordinar de mic. De aceea experimentările practice au confirmat probabilitatea
calculată teoretic: abaterile densității lui y de la cea uniformă sunt
neglijabile.
, ceva
extraordinar de mic. De aceea experimentările practice au confirmat probabilitatea
calculată teoretic: abaterile densității lui y de la cea uniformă sunt
neglijabile.
O ultimă
observație, înainte de a încheia această Anexă. Maxima lui von Mises, susținută
de Popper, că nu se pot trage concluzii probabiliste decât din premise probabiliste
mi se pare adevărată când se referă la experimentele clasice de probabilități
pe care le-am studiat mai sus. În cazul observării unui fenomen care se manifestă
sub forma unui șir aleator (în sensul că nu-i cunoaștem legea) de numere, și
asupra căruia nu putem interveni, poate că lucrurile nu stau chiar așa. Mă refer
la următorul exemplu ideal: pe o masă de biliard se mișcă, fără frecare și reflectându-se
de pereții mesei, o minge. Între reflectările de pereții mesei, ea se mișcă
rectiliniu și uniform, cu o viteză suficient de mare ca cel mult la 10 sec.
să se producă o ciocnire. Să presupunem că noi nu putem vedea acest lucru: un
aparat de fotografiat fotografiază din 10 sec. în 10 sec. poziția bilei la timpul
respectiv, iar noi nu putem interpreta decât fotografiile primite. Se demonstrează
în teoria ergodică faptul că dacă raportul între viteza inițială pe axa Ox și
cea pe axa Oy nu este rațional, atunci frecvențele apariției bilei într-o anumită
zonă a mesei de biliard vor fi, la limită, proporționale cu aria zonei. Cu alte
cuvinte, dacă am interpreta statistic fotografiile primite, vom fi constrânși
să deducem că punctul din fotografie este realizarea unui șir de variabile aleatoare
independente și uniform repartizate pe spațiul mesei de biliard (Vezi demonstrația
în Freiburger și ???).
Și totuși,
nu esre așa ! fenomenul este cât se poate de determinist.
Poate
că de multe ori, o abordare probabilistă este numai o soluție provizorie în
știință.
(*) În general, , 1) este unimodală; 2) ; 3)
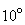 fiecare
(sau
fiecare
(sau 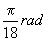 ). Sectoarele
sunt, alternativ, roșii și negre. Dacă ruleta se oprește pe negru, să spunem
că avem un succes; în caz contrar, avem un eșec. Ne propunem să calculăm probabilitățile
). Sectoarele
sunt, alternativ, roșii și negre. Dacă ruleta se oprește pe negru, să spunem
că avem un succes; în caz contrar, avem un eșec. Ne propunem să calculăm probabilitățile
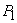 și
și
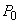 ale succesului
(respectiv eșecului). Poincaré presupune, într-o primă aproximație, că putem
neglija frecarea: roata capătă o viteză inițială de rotație
ale succesului
(respectiv eșecului). Poincaré presupune, într-o primă aproximație, că putem
neglija frecarea: roata capătă o viteză inițială de rotație 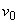 pe care
și-o menține până când este oprită brusc după T secunde. Unghiul
parcurs este egal, evident, cu
pe care
și-o menține până când este oprită brusc după T secunde. Unghiul
parcurs este egal, evident, cu 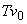 . Să presupunem
că
. Să presupunem
că 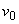 este o
variabilă aleatoare continuă, având o densitate de repartiție f despre
care nu mai este nevoie să presupunem nimic. Atunci densitatea de repartiție
a unghiului
este o
variabilă aleatoare continuă, având o densitate de repartiție f despre
care nu mai este nevoie să presupunem nimic. Atunci densitatea de repartiție
a unghiului 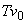 este
este
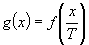 . Admițând
că ruleta pleacă tot timpul din aceeași poziție și că primul sector, în sens
trigonometric, care apare este cel roșu, avem (notând
. Admițând
că ruleta pleacă tot timpul din aceeași poziție și că primul sector, în sens
trigonometric, care apare este cel roșu, avem (notând 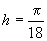 ):
):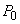
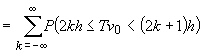
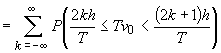
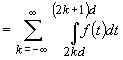 ,
,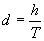 .
.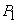
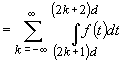
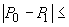
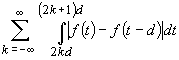
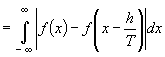
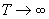 , ultima
cantitate converge la 0.
, ultima
cantitate converge la 0. 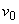 este uniform
frânată de o forță de frecare. Deci
este uniform
frânată de o forță de frecare. Deci 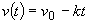 , unde
k este un coeficient de frecare. Presupunem că roata este lăsată până
se oprește singură. Acest lucru se va întâmpla când
, unde
k este un coeficient de frecare. Presupunem că roata este lăsată până
se oprește singură. Acest lucru se va întâmpla când 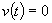 , deci
la timpul
, deci
la timpul 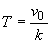 . Unghiul
parcurs după acest timp va fi egal cu
. Unghiul
parcurs după acest timp va fi egal cu 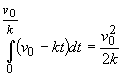 . Notând
acest unghi cu A, avem
. Notând
acest unghi cu A, avem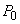
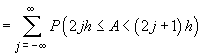
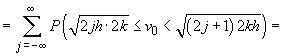
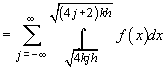
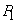
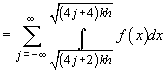 .
.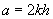 , rezultă:
, rezultă: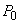 -
-
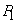
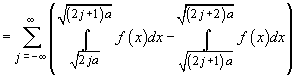 .
.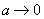
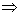
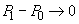 . Demonstrația
se va baza pe următorul rezultat:
. Demonstrația
se va baza pe următorul rezultat: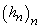 un șir
monoton de numere pozitive. Atunci:
un șir
monoton de numere pozitive. Atunci: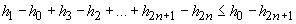 .
.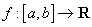 o funcție
continuă și
o funcție
continuă și 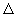
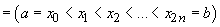 o diviziune
a intervalului
o diviziune
a intervalului 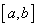 . Fie
. Fie
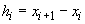 și
și
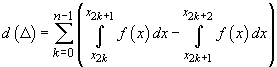 .
.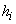 este monoton
și
este monoton
și 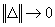 , rezultă
, rezultă
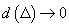 .
.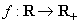 o densitate
de probabilitate și
o densitate
de probabilitate și 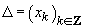 o diviziune
a lui R. Fie
o diviziune
a lui R. Fie 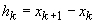 și
și
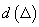 cu aceeași
definiție ca la 2., dar suma se extinde pentru toți
cu aceeași
definiție ca la 2., dar suma se extinde pentru toți 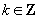 . Dacă
presupunem că
. Dacă
presupunem că 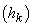 este un
șir monoton sau unimodal (crește până la un
este un
șir monoton sau unimodal (crește până la un 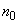 și apoi
scade), rămâne valabilă concluzia de la punctul 2.
și apoi
scade), rămâne valabilă concluzia de la punctul 2.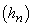 este crescător.
Atunci
este crescător.
Atunci 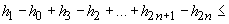
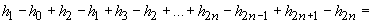
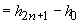 (termenii
se reduc doi câte doi)
(termenii
se reduc doi câte doi)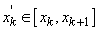 astfel
încât
astfel
încât 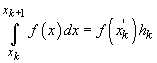 (teorema
Lagrange !). Fie
(teorema
Lagrange !). Fie 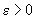 cu proprietatea
că
cu proprietatea
că 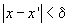
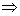
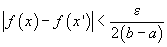 ( f
este uniform continuă !) și
( f
este uniform continuă !) și 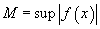 , norma
uniformă a lui f.
, norma
uniformă a lui f.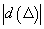
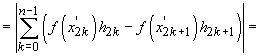
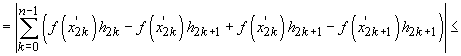
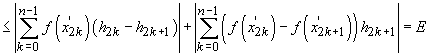
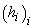 este descrescător
. În această situație norma diviziunii este
este descrescător
. În această situație norma diviziunii este 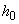 (altfel
ar fi
(altfel
ar fi 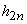 ) și, dacă
presupunem că
) și, dacă
presupunem că 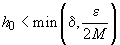 , expresia
E este mai mică decât
, expresia
E este mai mică decât 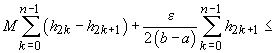
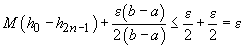 . Cum
. Cum
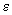 este arbitrar,
demonstrația este încheiată.
este arbitrar,
demonstrația este încheiată. era unimodală,
demonstrația nu se schimba prea mult. Estimarea 1. care a fost esențială devenea:
era unimodală,
demonstrația nu se schimba prea mult. Estimarea 1. care a fost esențială devenea: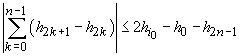 , unde
, unde
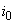 este acel
indice pentru care segmentul
este acel
indice pentru care segmentul 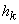 are lungime
maximă.
are lungime
maximă.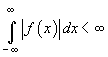 și pentru
orice
și pentru
orice 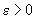 există
o altă funcție continuă g care este nulă în afara unui interval
există
o altă funcție continuă g care este nulă în afara unui interval
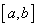 și cu
proprietatea că
și cu
proprietatea că 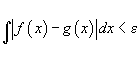 . După
majorarea
. După
majorarea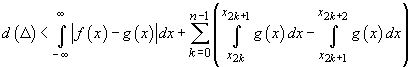 ,
,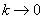
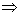
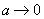
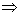
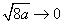 ; dar ultima
cantitate este exact norma diviziunii dată de punctele
; dar ultima
cantitate este exact norma diviziunii dată de punctele 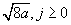 , care
apare în modelul propus. Deoarece, în plus
, care
apare în modelul propus. Deoarece, în plus 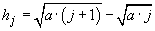 formează
un șir descrescător, rezultă că suntem în condițiile Lemei demonstrate (3.)
și deci
formează
un șir descrescător, rezultă că suntem în condițiile Lemei demonstrate (3.)
și deci 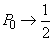 .
.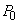 și
și
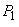 tind spre
tind spre
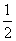 dacă T
tinde la
dacă T
tinde la 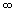 sau coefeicientul
de frecare tinde la 0, ceea ce spune cam același lucru: roata trebuie lăsată
să se învârtească cât mai mult. Dar în ce măsură explică aceasta echiprobabilitatea
rezultatelor ruletei ? Dacă abaterea de la
sau coefeicientul
de frecare tinde la 0, ceea ce spune cam același lucru: roata trebuie lăsată
să se învârtească cât mai mult. Dar în ce măsură explică aceasta echiprobabilitatea
rezultatelor ruletei ? Dacă abaterea de la 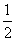 rămâne
foarte mare până când T este, de exemplu, de ordinul secolelor, explicația
devine, cu bunăvoință apreciind, iluzorie. În definitiv, am căzut în aceeași
capcană ca von Mises: postulăm relevanța unei limite la un experiment real.
Pentru fiecare T, în cadrul modelului simplificat al lui Poincaré, ne putem
imagina o repartiție a vitezei inițiale pe care crupierul o imprimă roții care
să aibă și densitatea continuă, dar să ne facă figura că
rămâne
foarte mare până când T este, de exemplu, de ordinul secolelor, explicația
devine, cu bunăvoință apreciind, iluzorie. În definitiv, am căzut în aceeași
capcană ca von Mises: postulăm relevanța unei limite la un experiment real.
Pentru fiecare T, în cadrul modelului simplificat al lui Poincaré, ne putem
imagina o repartiție a vitezei inițiale pe care crupierul o imprimă roții care
să aibă și densitatea continuă, dar să ne facă figura că 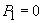 și
și
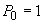 .
.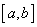 cu
cu
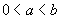 . Nu pare
o restricție nenaturală: în natură, majoritatea fenomenelor sunt, la o primă
aproximatie continui și este plauzibil de presupus că
. Nu pare
o restricție nenaturală: în natură, majoritatea fenomenelor sunt, la o primă
aproximatie continui și este plauzibil de presupus că 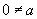 (dacă
viteza de rotație a roții este prea mică (de ordinul miimilor de grad pe secundă)
e normal să cerem alt joc, bănuind pe crupier de cârdășie cu banca și intenții
necinstite) și că există o limită fizică a vitezei de rotație pe care o poate
imprima ruletei. Până acum nu am avansat nici un pas pe drumul estimării vitezei
de convergență. Dar să admitem că cunoaștem modulul de continuitate al densității
f (adică, pentru fiecare
(dacă
viteza de rotație a roții este prea mică (de ordinul miimilor de grad pe secundă)
e normal să cerem alt joc, bănuind pe crupier de cârdășie cu banca și intenții
necinstite) și că există o limită fizică a vitezei de rotație pe care o poate
imprima ruletei. Până acum nu am avansat nici un pas pe drumul estimării vitezei
de convergență. Dar să admitem că cunoaștem modulul de continuitate al densității
f (adică, pentru fiecare 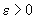 știm să
calculăm
știm să
calculăm 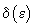 cu proprietatea
că
cu proprietatea
că 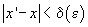
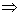
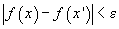 ). Atunci,
deoarece
). Atunci,
deoarece 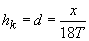 ,
,
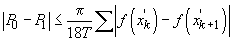 și
și
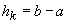 , dacă
vrem ca
, dacă
vrem ca 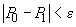 , trebuie
ales
, trebuie
ales 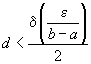 , deoarece
, deoarece
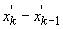 nu poate
depăși valoarea
nu poate
depăși valoarea 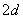 . Deci
. Deci
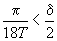 sau
sau
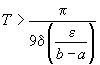 .
.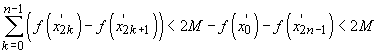 .
.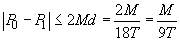 . Dacă
vrem ca această valoare să fie mai mică decât
. Dacă
vrem ca această valoare să fie mai mică decât 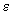 , trebuie
ca
, trebuie
ca 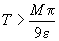 . În cazul
acesta nu mai este nevoie ca f să fie continuă cu suport compact: estimarea
. În cazul
acesta nu mai este nevoie ca f să fie continuă cu suport compact: estimarea
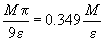 (1) este
valabilă pentru orice densitate f unimodală.
(1) este
valabilă pentru orice densitate f unimodală.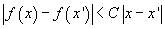 . Dacă
densitatea f este Lipschitziană de modul C, atunci
. Dacă
densitatea f este Lipschitziană de modul C, atunci 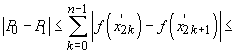
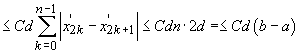 (deoarece
(deoarece
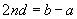 )
)
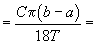
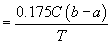 ; deci
(???? pag. 142) ca ultima cantitate să fie mai mică decât
; deci
(???? pag. 142) ca ultima cantitate să fie mai mică decât 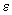 , trebuie
ca
, trebuie
ca 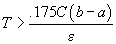 . (2)
. (2)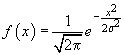 repartiția
normală centrată în 0 și de dispersie
repartiția
normală centrată în 0 și de dispersie 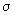 . Calculând
maximul primei derivate găsim
. Calculând
maximul primei derivate găsim 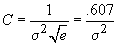 . Cât despre
M, el este egal cu
. Cât despre
M, el este egal cu 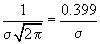 . Folosind
estimarea (1), găsim
. Folosind
estimarea (1), găsim 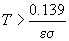 , iar folosind
pe (2) găsim
, iar folosind
pe (2) găsim 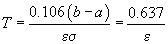 deoarece
putem lua
deoarece
putem lua 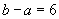 ???
se știe că în cazul unei variabile normale probabilitatea abaterilor cu mai
mult decât
???
se știe că în cazul unei variabile normale probabilitatea abaterilor cu mai
mult decât 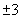 de la
media m este sub 1%. Deși pentru anumite valori ale lui ??? prima
estimare dă rezultate superioare, a doua nu depinde de ???.
de la
media m este sub 1%. Deși pentru anumite valori ale lui ??? prima
estimare dă rezultate superioare, a doua nu depinde de ???.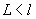 se aruncă
pe o rețea de drepte echidistante situate la distanța l una de alta.
Se cere calcularea probabilității ca acul să intersecteze vreuna din dreptele
rețelei.
se aruncă
pe o rețea de drepte echidistante situate la distanța l una de alta.
Se cere calcularea probabilității ca acul să intersecteze vreuna din dreptele
rețelei. Să considerăm un sistem rectangular de axe xOy
în care dreptele rețelei să fie
Să considerăm un sistem rectangular de axe xOy
în care dreptele rețelei să fie 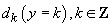 . Putem
răspunde la întrebarea dacă acul intersectează vreuna din dreptele
. Putem
răspunde la întrebarea dacă acul intersectează vreuna din dreptele 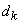 cunoscând
doar doi parametri: ordonata mijlocului acului
cunoscând
doar doi parametri: ordonata mijlocului acului 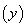 și unghiul
format de ac cu dreptele
și unghiul
format de ac cu dreptele 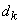 . Atunci,
după cum se vede în figura alăturată, acul intersectează una din drepte dacă
și numai dacă
. Atunci,
după cum se vede în figura alăturată, acul intersectează una din drepte dacă
și numai dacă  sau dacă
sau dacă
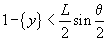 .
.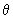 și sunt
variabile aleatoare independente având densitățile de repartiție
și sunt
variabile aleatoare independente având densitățile de repartiție 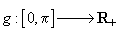 , respectiv
, respectiv
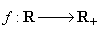 . Probabilitatea
căutată este
. Probabilitatea
căutată este 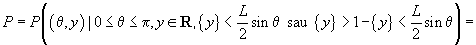
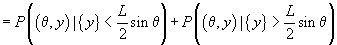
 deoarece cele două evenimente sunt incompatibile
deoarece cele două evenimente sunt incompatibile
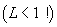 . Remarcând
că aceasta reprezintă probabilitatea suprafețelor hașurate din Fig.2, găsim
că
. Remarcând
că aceasta reprezintă probabilitatea suprafețelor hașurate din Fig.2, găsim
că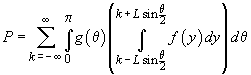 .
. cât și
cât și
 sunt repartizate
uniform pe intervalele
sunt repartizate
uniform pe intervalele 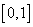 respectiv
respectiv
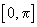 . Cu aceste
. Cu aceste
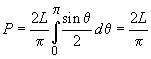 . Dacă
. Dacă
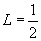 , rezultă
că
, rezultă
că 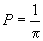 .
.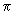 . La o
primă vedere, s-ar părea că nu trebuie să fim prea optimiști asupra rezultatului,
deoarece probabilitatea teoretică a fost obținută în niște ipoteze foarte restrictive.
Nu este așa. Este, din contră, surprinzător că estimările lui
. La o
primă vedere, s-ar părea că nu trebuie să fim prea optimiști asupra rezultatului,
deoarece probabilitatea teoretică a fost obținută în niște ipoteze foarte restrictive.
Nu este așa. Este, din contră, surprinzător că estimările lui 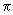 făcute
pe această bază s-au dovedit foarte bune ! Tabelul următor este edificator:
făcute
pe această bază s-au dovedit foarte bune ! Tabelul următor este edificator: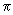
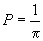 ? Explicația
trebuie să fie că în ipoteze foarte generale asupra lui y partea sa zecimală
tinde să fie uniform repartizată. Ipoteza că
? Explicația
trebuie să fie că în ipoteze foarte generale asupra lui y partea sa zecimală
tinde să fie uniform repartizată. Ipoteza că 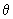 este și
el repartizat uniform pe intervalul
este și
el repartizat uniform pe intervalul 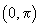 nu mi
se pare atât de nenaturală,căci este de așteptat ca aruncând un ac, unghiul
să nu aibă vreo direcție privilegiată. Din contră, nu este natural să admit
că mijlocul său să nu aibă vreo preferință, o zonă privilegiată în care să cadă.
Dacă arunc o piatră la întâmplare, este sigur că ea va cădea undeva în interioruk
cercului având ca centru locul în care mă aflu și o rază de 100 m). De aceea
este mai natural să admit că y este o variabilă aleatoare repartizată
nu mi
se pare atât de nenaturală,căci este de așteptat ca aruncând un ac, unghiul
să nu aibă vreo direcție privilegiată. Din contră, nu este natural să admit
că mijlocul său să nu aibă vreo preferință, o zonă privilegiată în care să cadă.
Dacă arunc o piatră la întâmplare, este sigur că ea va cădea undeva în interioruk
cercului având ca centru locul în care mă aflu și o rază de 100 m). De aceea
este mai natural să admit că y este o variabilă aleatoare repartizată
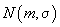 cu o anumită
medie m și dispersie
cu o anumită
medie m și dispersie 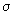 . În acest
caz conjectura se verifică: dacă
. În acest
caz conjectura se verifică: dacă 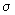 nu este
exagerat de mic,
nu este
exagerat de mic, 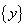 este aproape
uniform repartizat, după cum se arată în următorul rezultat splendid, demonstrat
de S. Teleman (comunicare personală):
este aproape
uniform repartizat, după cum se arată în următorul rezultat splendid, demonstrat
de S. Teleman (comunicare personală):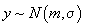 , atunci
, atunci
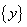 are de
asemenea o repartiție de probabilitate absolut continuă cu densitatea
are de
asemenea o repartiție de probabilitate absolut continuă cu densitatea
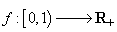 având
proprietatea că
având
proprietatea că 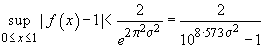
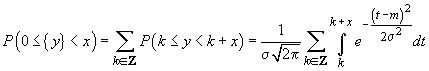 .
.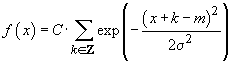 . Funcția
f are sens pentru orice
. Funcția
f are sens pentru orice 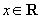 ; ea este,
în plus, periodică și are perioadă 1. Am notat
; ea este,
în plus, periodică și are perioadă 1. Am notat 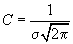 . Să notăm
. Să notăm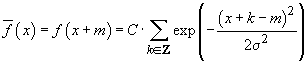 și
și
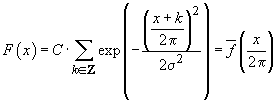 .
.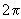 . Fiind
și continuă, se poate dezvolta în serie Fourier
. Fiind
și continuă, se poate dezvolta în serie Fourier 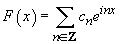 , unde
coeficienții Fourier
, unde
coeficienții Fourier 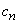 sunt dați
de expresia
sunt dați
de expresia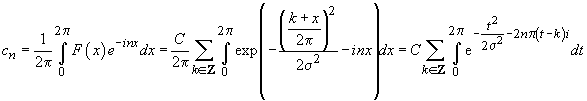

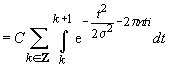
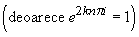
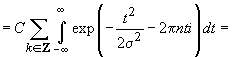
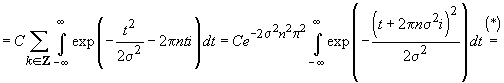
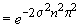 (deoarece
ulrima integrală este egală exact cu
(deoarece
ulrima integrală este egală exact cu 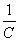 ).
).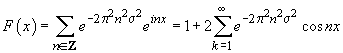 și astfel
și astfel
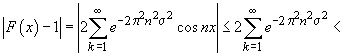
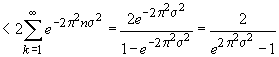 q.e.d.
q.e.d.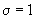 , atunci
abaterea densității f de la 1 este de ordinul lui
, atunci
abaterea densității f de la 1 este de ordinul lui 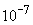 ; pentru
; pentru
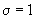 , ea devine
, ea devine
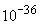 , ceva
extraordinar de mic. De aceea experimentările practice au confirmat probabilitatea
calculată teoretic: abaterile densității lui y de la cea uniformă sunt
neglijabile.
, ceva
extraordinar de mic. De aceea experimentările practice au confirmat probabilitatea
calculată teoretic: abaterile densității lui y de la cea uniformă sunt
neglijabile.