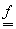 orice
șir de funcții
orice
șir de funcții 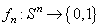 .
.ANEXA 4. Axiomatizări ale calculului probabilităților
1. Von Mises, 1919 (din [38])
Definiția 1. Fie S
o mulțime oarecare. Se numește selecție de loc, notată 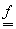 orice
șir de funcții
orice
șir de funcții 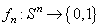 .
.
Definiția 2. Fie
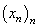 un șir
cu valori în S, și
un șir
cu valori în S, și 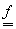 o selecție
de loc. Notăm
o selecție
de loc. Notăm 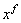 subșirul
extras din x după următorul porcedeu:
subșirul
extras din x după următorul porcedeu: 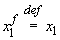 ,
,
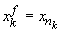 , unde
, unde
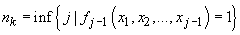 ,
,
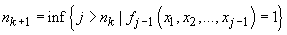
Definiția 3. Fie S
o mulțime oarecare,  o familie
de părți ale lui S închisă la complementare și reuniune numărabilă (
o familie
de părți ale lui S închisă la complementare și reuniune numărabilă (
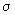 - algebră)
și G o familie numărabilă de selecții de loc. Șirul
- algebră)
și G o familie numărabilă de selecții de loc. Șirul 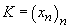 de elemente
din S se numește
de elemente
din S se numește 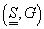 - colectiv
dacă
- colectiv
dacă
(i)
pentru orice mulțime
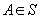 , există
, există
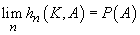 , unde
, unde
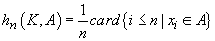
(ii)
pentru orice selecție
f din G, 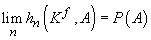 .
.
Definiția 4.
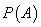 se numește
probabilitatea evenimentului A.
se numește
probabilitatea evenimentului A.
Definiția 5. Fie
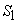 și
și
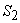 două mulțimi
oarecare,
două mulțimi
oarecare, 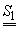 și
și
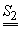 două
două
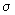 - algebre
pe ele și G o familie numărabilă de selecții de loc. Fie
- algebre
pe ele și G o familie numărabilă de selecții de loc. Fie 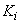 (
(
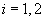 )
)
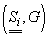 - colective.
- colective.
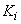 se numesc
colective independente dacă
se numesc
colective independente dacă 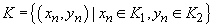 este un
este un
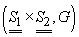 colectiv
și
colectiv
și 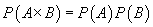 pentru
orice
pentru
orice 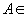
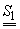 ,
,
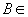
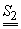 .
.
2. Ramsey, 1926 ([ ])
Fie x un subiect epistemic. Se consideră noțiuni primare și nu se definesc, utilitatea (goods) și indiferența.
Definiția 1. Propoziția p se numește etic neutră dacă ea nu este obiect de dorință sau respingere din partea lui x.
Definiția
2. Fie A, B două utilități și p o propoziție etic neutră. Sistemul
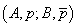 se numește
alternativă dacă: x primește A dacă p este adevărat și
B dacă p este fals.
se numește
alternativă dacă: x primește A dacă p este adevărat și
B dacă p este fals.
Definiția
3. x are încredere 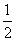 în p
(notație:
în p
(notație: 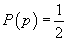 ) dacă
pentru orice două utilități A și B alternativele
) dacă
pentru orice două utilități A și B alternativele 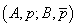 sau
sau
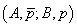 îi sunt
indiferente.
îi sunt
indiferente.
Axioma
1. Există o aplicație 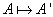 care atribuie
fiecărei utilități un număr real numit valoarea ei. Aplicația de valorizare
are proprietatea că dacă p este etic neutră și
care atribuie
fiecărei utilități un număr real numit valoarea ei. Aplicația de valorizare
are proprietatea că dacă p este etic neutră și 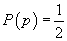 ,
,
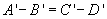
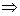 pentru
x alternativele
pentru
x alternativele 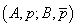 sau
sau
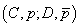 îi sunt
indiferente.
îi sunt
indiferente.
Axioma
2. Există propoziții etic neutre p ca 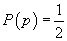 .
.
Definiția
4. Dacă x nu preferă între A (sigur) și 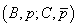 definim
definim
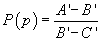 ; definiția
nu este contradictorie și
; definiția
nu este contradictorie și 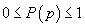 .
.
Definiția
5. Dacă lui x îi este indiferent între 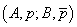 sau
sau
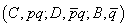 definim
definim
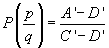 .
.
Teoremă.
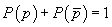 ;
;
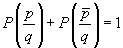 ;
;
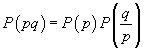 ;
;
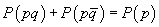 .
.
3. Reichenbach, 1932 ([49])
Fie
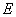 o algebră
Boole și
o algebră
Boole și 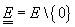 ( 0 = elementul zero al algebrei Boole).
Aplicația
( 0 = elementul zero al algebrei Boole).
Aplicația 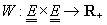 se numește
probabilitate dacă
se numește
probabilitate dacă
(i)
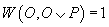 ,
,
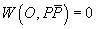 pentru
orice
pentru
orice 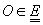 și
și
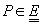 ;
;
(ii)
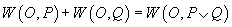 , dacă
, dacă
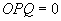 ;
;
(iii)
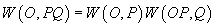 pentru
orice elemente pentru care
pentru
orice elemente pentru care 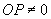
Interpretarea
geometrică: 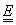 este o
algebră de părți a lui E,
este o
algebră de părți a lui E, 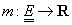 este o
măsură aditivă și
este o
măsură aditivă și 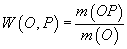 , dacă
, dacă
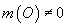 .
.
Interpretarea
frecvențială. Fie 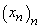 și
și
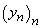 două șiruri.
Fie
două șiruri.
Fie 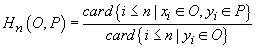 . Dacă
. Dacă
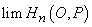 există,
notăm această limită cu
există,
notăm această limită cu 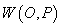 . Ea satisface
axiomele (i), (ii), (iii).
. Ea satisface
axiomele (i), (ii), (iii).
4. Kolmogorov, 1933 ([19])
Definiția 1. Tripletul 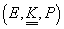 se numește
spațiu probabilizat dacă
se numește
spațiu probabilizat dacă
(i) E este o mulțime oarecare.
(ii)
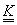 este o
este o
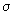 - algebră
de părți ale lui E.
- algebră
de părți ale lui E.
(iii) 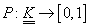 o funcție
de mulțime cu proprietatea că
o funcție
de mulțime cu proprietatea că 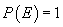 și pentru
orice șir
și pentru
orice șir 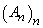 de mulțimi
disjuncte din
de mulțimi
disjuncte din 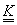 ,
,
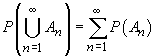
Definiția 2. Perechea 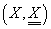 unde X
este o mulțime oarecare și
unde X
este o mulțime oarecare și 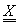 o
o
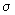 - algebră
pe X se numește spațiu măsurabil.
- algebră
pe X se numește spațiu măsurabil.
Definiția 3. Fie 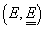 și
și
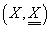 două spații
măsurabile.
două spații
măsurabile. 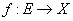 se numește
variabilă aleatoare dacă
se numește
variabilă aleatoare dacă 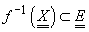 .
.
Definiția 4. Fie 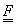 ,
,
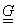 două sub-
două sub-
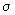 -algebre
ale lui
-algebre
ale lui 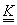 .
.
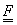 și
și
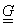 se numesc
independente dacă
se numesc
independente dacă 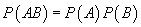 pentru
orice
pentru
orice 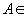
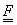 și
și
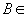
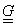 .
.
Definiția 5. Fie 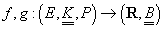 două variabile
aleatoare reale (
două variabile
aleatoare reale ( 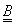 ) este
algebra mulțimilor de pe R care este generată de intervalele deschise
așa numita
) este
algebra mulțimilor de pe R care este generată de intervalele deschise
așa numita 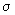 -algebră
boreliană de pe R). f și g se numesc independente dacă
-algebră
boreliană de pe R). f și g se numesc independente dacă
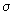 -algebrele
-algebrele
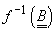 și
și
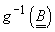 sunt independente.
sunt independente.
Definiția 6. Fie 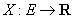 o variabilă
aleatoare reală. Probabilitatea
o variabilă
aleatoare reală. Probabilitatea 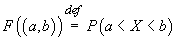 se numește
repartiția lui X. Ea se identifică cu funcția sa de repartiție
se numește
repartiția lui X. Ea se identifică cu funcția sa de repartiție
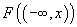 . Dacă
. Dacă
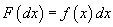 , se zice
că X este o v.a. absolut continuă și f se numește densitatea sa
de repartiție.
, se zice
că X este o v.a. absolut continuă și f se numește densitatea sa
de repartiție.
5. Popper, 1938, 1955 ([47], pag. 312)
Fie S
o latice complementată cel mult numărabilă și 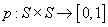 cu proprietățile
cu proprietățile
A1. Există 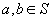 astfel
încât
astfel
încât 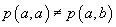 .
.
A2. Dacă 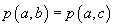 atunci
există
atunci
există 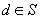 astfel
încât
astfel
încât 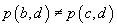 .
.
A3. 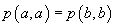 pentru
orice
pentru
orice 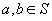 .
.
B1. 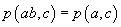 pentru
orice
pentru
orice 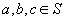 .
.
B2. 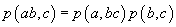 pentru
orice
pentru
orice 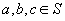 .
.
C1. 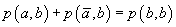 cu excepția
cazului în care
cu excepția
cazului în care 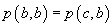 pentru
orice
pentru
orice 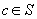 .
.
Definiția
probabilității absolute. Dacă 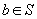 are proprietatea
că
are proprietatea
că 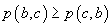 pentru
orice
pentru
orice 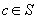 , definim
, definim
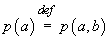 .
.
6. De Finetti, 1937
Fie
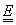 o algebră
Boole de evenimente. Evenimentul imposibil se notează cu
o algebră
Boole de evenimente. Evenimentul imposibil se notează cu 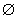 și cel
sigur cu 1; fie, de asemenea, x un subiect epistemic.
și cel
sigur cu 1; fie, de asemenea, x un subiect epistemic.
Ax
1. Există pe 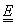 o relație
de preordine totală notată
o relație
de preordine totală notată 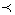 care
satisface relația
care
satisface relația 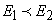 ,
,
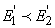
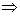
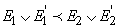 pentru
orice
pentru
orice 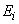 ,
,
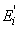 cu proprietatea
că
cu proprietatea
că 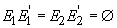 . Relația
. Relația
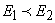 se citește
se citește
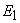 nu este
mai probabil ca
nu este
mai probabil ca 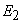
Ax
2. Există o a doua relație de preordine totală notată 
între toate perechile
între toate perechile 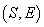 , unde
S este o sumă de bani și E un eveniment, care se citește
, unde
S este o sumă de bani și E un eveniment, care se citește
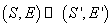 Suma
S dacă apare E este preferabilă sumei S dacă apare E . Dacă
Suma
S dacă apare E este preferabilă sumei S dacă apare E . Dacă
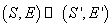 și
și
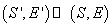 , spunem
că între cele două perechi se manifest indiferență.
, spunem
că între cele două perechi se manifest indiferență.
Axioma
3 Definiția 1. Pentru orice 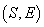 există
un număr
există
un număr 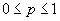 care nu
depinde decât de E, nu și de S astfel încât x manifestă
indiferență între
care nu
depinde decât de E, nu și de S astfel încât x manifestă
indiferență între 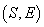 și
și
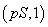 ; p
se notează
; p
se notează 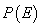 și se
numește probabilitatea atașată de x lui E.
și se
numește probabilitatea atașată de x lui E.
Ax
4. Principiul pariului echitabil (al coerenței). Fie 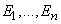 evenimente
oarecare. Probabilitățile oricărui eveniment care rezultă dintr-o combinare
a lor trebuie date astfel încât să nu se permită unui eventual opozant să câștige
un pariu asupra lor în toate cazurile posibile.
evenimente
oarecare. Probabilitățile oricărui eveniment care rezultă dintr-o combinare
a lor trebuie date astfel încât să nu se permită unui eventual opozant să câștige
un pariu asupra lor în toate cazurile posibile.
Definiția
5. Fie E și E două evenimente. Dacă x manifestă
indiferență între 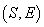 și
și
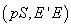 și p
nu depinde decât de E și E, definim
și p
nu depinde decât de E și E, definim 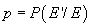 și o numim
probabilitatea lui E
condiționată de E .
și o numim
probabilitatea lui E
condiționată de E .
Teoremă.
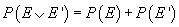 pentru
orice evenimente incompatibile E și E. În plus,
pentru
orice evenimente incompatibile E și E. În plus, 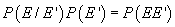 întotdeauna.
întotdeauna.
Definiția
6. Șirul de evenimente 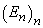 se interșanjabil
dacă pentru orice
se interșanjabil
dacă pentru orice 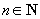 și orice
sistem de numere naturale distincte
și orice
sistem de numere naturale distincte 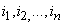
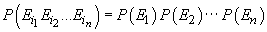 .
.
Apoi se arată că toate teoremele importante care se demonstrează ??? pentru evenimentele independente se pot demonstra și în ipoteza interșanjabilității.
7. Probabilitatea dialectică (Bodiou, 1964 / /, )
Fie T
o latice (adică pe T există o relație de ordine față de care orice pereche
 S ???
admite
S ???
admite  ) și
) și
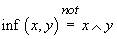 ) relativ
autocomplementată (există un automorfism
) relativ
autocomplementată (există un automorfism 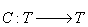 ca
ca
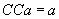 și
și
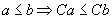 pentru
orice
pentru
orice 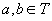 ; în plus,
pentru orice a b există
; în plus,
pentru orice a b există 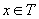 ca
ca
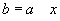 ), în care
), în care
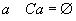 pentru
orice
pentru
orice 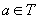 . T
se numește latice dialectică.
. T
se numește latice dialectică.
Def.
1. Fie T o latice dialectică. Elementele a și b se
numesc ortogonale dacă 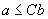 .
.
Def.
2. Fie T o latice dialectică. Aplicația 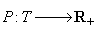 se numește
probabilitate dialectică dacă
se numește
probabilitate dialectică dacă 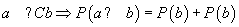 . Dacă
pentru orice șir
. Dacă
pentru orice șir 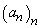 de elemente
din T reciproc ortogonale avem
de elemente
din T reciproc ortogonale avem 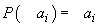 se spune
că P este o probabilitate complet dialectică. În plus, o probabilitate
mai satisface condiția
se spune
că P este o probabilitate complet dialectică. În plus, o probabilitate
mai satisface condiția 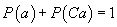 pentru
orice
pentru
orice 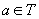 .
.
Def.
3. Sublaticea 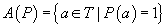 se numește
laticea de adecvare a lui P.
se numește
laticea de adecvare a lui P.
Def.
4. 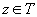 se numește
atom dacă
se numește
atom dacă 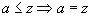 sau
sau
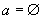 .
.
Axiomă.
Orice atom z determină o probabilitate condiționată 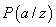
Def.
5. Dacă 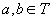 se notează
se notează
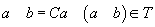 și se
numește implicatorul lui b din a.
și se
numește implicatorul lui b din a.
Def.
6. Condiționare dialectică. Fie 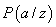 o probabilitate
atomică dată de z și
o probabilitate
atomică dată de z și 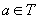 . Orice
probabilitate
. Orice
probabilitate 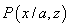 se numește
probabilitate condiționată de a dacă
se numește
probabilitate condiționată de a dacă 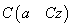 aparține
laticii sale de adecvare. Atunci ea este de asemenea atomică, determinată de
atomul
aparține
laticii sale de adecvare. Atunci ea este de asemenea atomică, determinată de
atomul 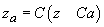 . În plus
atomul
. În plus
atomul 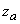 este unic
determinat de relația
este unic
determinat de relația 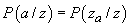 .
.
Teoremă.
Dacă T este algebră Boole, definiția probabilității coincide cu cea
clasică. Necesar și suficient ca 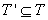 să fie
algebră Boole este ca pentru orice atom
să fie
algebră Boole este ca pentru orice atom 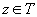 și orice
și orice
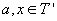 să fie
valabilă teorema de înmulțire a probabilităților:
să fie
valabilă teorema de înmulțire a probabilităților: 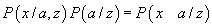 .
.
Def.
7. Aplicația 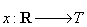 s.n. variabilă
aleatoare reală dacă:
s.n. variabilă
aleatoare reală dacă:
(i)
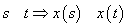 și
și
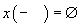 ,
,
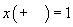 (1=elementul
maximal);
(1=elementul
maximal);
(ii)
pentru orice atom 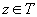 ,
,
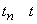
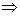
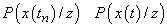 .
.
8. Probabilitatea cuantică (Bodiou, 1964)
Fie X
un spațiu Hilbert și  . Fie
. Fie
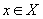 oarecare
ca
oarecare
ca 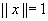 . Cuplul
. Cuplul
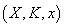 se numește
spațiu probabilistic cuantic generat de atomul x. Dacă
se numește
spațiu probabilistic cuantic generat de atomul x. Dacă 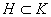 , definim
, definim
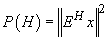 , unde
, unde
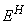 este operatorul
de proiecție ortogonală pe H.
este operatorul
de proiecție ortogonală pe H.
Teoremă.
Dacă 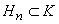 sunt ortogonale,
atunci
sunt ortogonale,
atunci 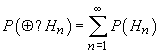 . În plus,
. În plus,
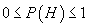 .
.
Definiție
2. Fie 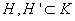 . Definim
. Definim
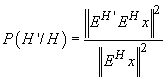 .
.
Observație.
In 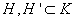 . Definim
. Definim
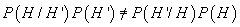 , spre
deosebire de teoria clasică. De aceea, aceste probabilități se numesc necomutative.
, spre
deosebire de teoria clasică. De aceea, aceste probabilități se numesc necomutative.
Definiție.
Dacă se verifică teorema înmulțirii 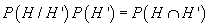 se spune
că H și H sunt compatibile. Acest lucru se întâmplă dacă
și numai dacă proiectorii
se spune
că H și H sunt compatibile. Acest lucru se întâmplă dacă
și numai dacă proiectorii 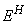 și
și
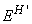 comută
comută
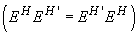 .
.
9. Probabilități pe algebre și algebre Boole (O. Onicescu, I. Cuculescu, în / /)
Definiție.
Fie E o algebră Boole (respectiv - algebră Boole). Aplicația 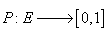 este probabilitate
(respectiv -probabilitate) dacă
este probabilitate
(respectiv -probabilitate) dacă 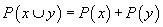 dacă
dacă
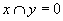 (respectiv
(respectiv
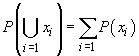 ) dacă
) dacă
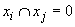 pentru
pentru
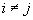 și, în
plus,
și, în
plus, 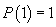 .
.
Definiție.
Familia de sub-algebre Boole 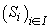 se numește
independentă dacă pentru orice n și orice
se numește
independentă dacă pentru orice n și orice 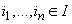 și
și
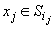 avem
avem
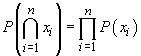 . Perechea
. Perechea
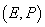 se numește
câmp.
se numește
câmp.
Analogul variabilelor aleatoare sunt funcțiile sumă.
Definiție.
Fie 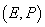 un câmp.
Funcția
un câmp.
Funcția 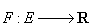 se numește
funcție sumă dacă este aditivă (respectiv, în cazul - algebrelor Boole) aditivă și absolut continuă față de P
(
se numește
funcție sumă dacă este aditivă (respectiv, în cazul - algebrelor Boole) aditivă și absolut continuă față de P
( 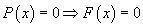 ).
).
Matematicienii
români au realizat multe din teoriile axiomatizării clasice (Kolmogorov) pe
algebre Boole (teorie ergodică, entropie, informație - Onicescu); spații
 (Marinescu);
martingale și procese Markov (Onicescu); analiză funcțională pe latici Boole
(Cristescu, Sâmboan) etc.
(Marinescu);
martingale și procese Markov (Onicescu); analiză funcțională pe latici Boole
(Cristescu, Sâmboan) etc.
O altă direcție de lucru pe algebre Boole este dată de școala de la Tașkent (Sarîmsakov, Ajupov, Kucikarov); ideea lor este să se axiomatizeze direct spațiul variabilelor aleatoare, în care mulțimile se identifică cu idempotenții unui semicâmp topologic (Vezi / /).
10. Sisteme axiomatice calitative (Koopman, 1940; Suppes, 1971).
Deoarece sunt foarte asemănătoare, ne vom mulțumi cu prezentarea axiomatizării Suppes pentru Propensități (/ /, pg. 519)
Definiția
1. Tripletul 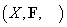 se numește
structura calitativă de probabilitate condiționată, dacă:
se numește
structura calitativă de probabilitate condiționată, dacă:
I. X este o mulțime oarecare, iar F este o algebră de părți ale lui X.
Elementele A, B, ... din F se interpretează ca evenimente sau rezultate ale unui context experimental.
II.
este o relație pe mulțimea 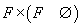 ; notația
; notația
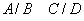
se interpretează
ca tendința lui A de a se produce dacă s+a produs B este cel
puțin la fel de mare ca cea a lui C dacă s-a produs D. Din ea se deduc alte
două relații: cea strictă 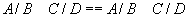 dar
dar
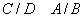 și echivalența
și echivalența
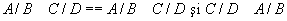 .
.
Între ele postulează următoarele relații:
1.
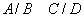 și
și
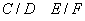
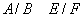
2.
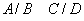 sau
sau
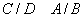 ;
;
3.
 ;
;
4.
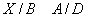
5.
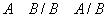
6. Dacă
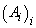 și
și
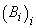 sunt disjuncte
și
sunt disjuncte
și 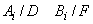
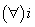 , atunci
, atunci
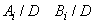 . În plus,
dacă există i ca
. În plus,
dacă există i ca 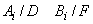 , atunci
, atunci
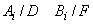 ;
;
7. Dacă
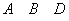 ,
,
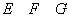 ,
,
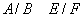 ,
,
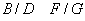 , atunci
, atunci
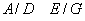 . În plus,
. În plus,
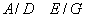 cu excepția
cazurilor
cu excepția
cazurilor 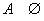 sau
sau
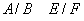 ,
,
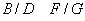 ;
;
8. Dacă
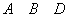 ,
,
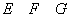 ,
,
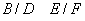 și
și
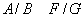 , atunci
, atunci
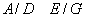 . În plus,
dacă în premise apare pe undeva , la fel se întâmplă și la concluzie.
. În plus,
dacă în premise apare pe undeva , la fel se întâmplă și la concluzie.
Definiția
2. Structura calitativă 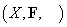 se numește
arhimediană dacă orice șir
se numește
arhimediană dacă orice șir 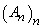 cu proprietatea
că
cu proprietatea
că 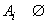 ,
,
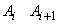 și
și
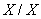 ,
,
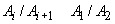 este finit.
este finit.
Se demonstrează
apoi că în anumite condiții suplimentare, există o probabilitate pe F,
obișnuită, ca 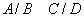
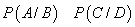 .
.
11. Drieschner, 1979 (/ /).
Fie un
context experimental X și o teorie fizică
T. Fie 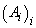 alternativa
prevăzută de teorie. Atunci
alternativa
prevăzută de teorie. Atunci 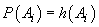 = frecvența
relativă prevăzută a apariției rezultatului
= frecvența
relativă prevăzută a apariției rezultatului 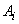 se numește
probabilitatea lui
se numește
probabilitatea lui 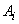 . Fiecare
alternativă generează o algebră Boole. Două alternative pot să nu fie compatibile
între ele, cum este cazul în mecanica cuantică, și atunci nu are sens să vorbim
despre
. Fiecare
alternativă generează o algebră Boole. Două alternative pot să nu fie compatibile
între ele, cum este cazul în mecanica cuantică, și atunci nu are sens să vorbim
despre 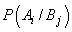 . În cazul
în care are sens să se discute despre
. În cazul
în care are sens să se discute despre 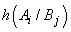 se subânțelege
că alternativele A și B sunt compatibile cuantic, deci aparțin
unei aceleiași algebre Boole mai mare; în acest din urmă caz funcționează legile
calculului clasic al probabilității simplu aditive, înlocuind sistematic, cuvântul
probabilitate cu frecvență relativă prevăzută.
se subânțelege
că alternativele A și B sunt compatibile cuantic, deci aparțin
unei aceleiași algebre Boole mai mare; în acest din urmă caz funcționează legile
calculului clasic al probabilității simplu aditive, înlocuind sistematic, cuvântul
probabilitate cu frecvență relativă prevăzută.
Studierea interrelațiilor între aceste 11 sisteme formale depășește scopul lucrării de față.